For the above cell
The correct Answer is:B
To solve the problem regarding the electrochemical cell, we need to calculate the cell potential (E_cell) and the Gibbs free energy change (ΔG) based on the given concentrations of the ions involved. Let's break it down step by step.
Step 1: Identify the Cell Reactions
In an electrochemical cell, we have two half-reactions: one at the anode and one at the cathode. The anode is where oxidation occurs, and the cathode is where reduction occurs.
Assuming the cell is represented as:
M+(0.05M)|M+(1M)
The half-reactions can be represented as:
- Anode (oxidation): M→M++e−
- Cathode (reduction): M++e−→M
Step 2: Calculate the Standard Cell Potential (E°)
Given that the standard reduction potential (E°) for the half-reaction is 0 V (as stated in the video), we can use the Nernst equation to find the cell potential (E_cell).
Step 3: Apply the Nernst Equation
The Nernst equation is given by:
E=E∘−RTnFlnQ
Where:
- E = cell potential
- E∘ = standard cell potential (0 V in this case)
- R = universal gas constant (8.314 J/(mol·K))
- T = temperature in Kelvin (assume 298 K if not provided)
- n = number of moles of electrons transferred (1 for this reaction)
- F = Faraday's constant (96485 C/mol)
- Q = reaction quotient
Step 4: Calculate the Reaction Quotient (Q)
The reaction quotient Q is given by:
Q=(M+)anode(M+)cathode=0.051=0.05
Step 5: Substitute Values into the Nernst Equation
Now substituting the values into the Nernst equation:
E=0−(8.314)(298)(1)(96485)ln(0.05)
Calculating the logarithm:
ln(0.05)≈−2.9957
Now substituting this back into the equation:
E=−(8.314)(298)96485×(−2.9957)
Calculating the value:
E≈(8.314)(298)(2.9957)96485
Step 6: Calculate ΔG
The relationship between ΔG and E_cell is given by:
ΔG=−nFE
Substituting the values:
ΔG=−1×96485×E
Step 7: Determine the Signs of E_cell and ΔG
From the calculations:
- If E is positive, then Ecell>0
- If ΔG is negative, then ΔG<0
Conclusion
Based on the calculations and the signs:
- Ecell>0
- ΔG<0
Thus, the correct option is D.
In an electrochemical cell, we have two half-reactions: one at the anode and one at the cathode. The anode is where oxidation occurs, and the cathode is where reduction occurs.
M+(0.05M)|M+(1M)
- Anode (oxidation): M→M++e−
- Cathode (reduction): M++e−→M
Given that the standard reduction potential (E°) for the half-reaction is 0 V (as stated in the video), we can use the Nernst equation to find the cell potential (E_cell).
The Nernst equation is given by:
E=E∘−RTnFlnQ
- E = cell potential
- E∘ = standard cell potential (0 V in this case)
- R = universal gas constant (8.314 J/(mol·K))
- T = temperature in Kelvin (assume 298 K if not provided)
- n = number of moles of electrons transferred (1 for this reaction)
- F = Faraday's constant (96485 C/mol)
- Q = reaction quotient
The reaction quotient Q is given by:
Q=(M+)anode(M+)cathode=0.051=0.05
Now substituting the values into the Nernst equation:
E=0−(8.314)(298)(1)(96485)ln(0.05)
ln(0.05)≈−2.9957
E=−(8.314)(298)96485×(−2.9957)
E≈(8.314)(298)(2.9957)96485
The relationship between ΔG and E_cell is given by:
ΔG=−nFE
ΔG=−1×96485×E
From the calculations:
- If E is positive, then Ecell>0
- If ΔG is negative, then ΔG<0
Based on the calculations and the signs:
- Ecell>0
- ΔG<0
Similar Questions
The following chemical reaction is occurring in an electrochemical cell
Mg(s)+2Ag+(0.0001M)→Mg2+(0.10M)+2Ag(s)
The E° electrode values are
Mg2+/Mg=−2.36V,
Ag+/Ag=0.81V
For lids cell calculate/write
(a) (i) E° value for the electrode 2Ag+/2Ag
(ii) Standard cell potential E∘cell
(b) Cell potential Ecell ,
(c) (i) Symbolic representation of the above cell.
(ii) Will the above cell reaction be spontaneous ?View SolutionThe following chemical reaction occurring in an electrochemical cell :
Mg(s)+2Ag+(0.0001M)→Mg2+(0.10M)+2Ag(s)
Given E∘Mg2+/Mg=−2.36 V,E∘Ag+/Ag=+0.81 V
For the cell, calculate/write :
(i) E∘ value for the electrode 2Ag+/2Ag
(ii) Standard cell potential (E∘)
(iii) Cell potential (E)
(iv) Give the symbolic representation of the above cell
(v) Will the above cell reaction be spontaneous ?View Solution
Knowledge Check
- Question 1 - Select One
Zn∣∣Zn2+(a=0.1M)∣∣∣∣Fe2+(a=0.01M)∣∣Fe.
The emf of the above cell is 0.2905V. Equilibrium constant for the cell reaction isA100.32/0.059B100.32/0.0295C100.26/0.0295D100.32/0.295 - Question 2 - Select One
Zn∣∣Zn2+(a=0.1M)∣∣∣∣Fe2+(a=0.01M)∣∣Fe
the emf of the above cell is 0.2905 V Equilibrium constant for the cell reaction isA100.32/0.591B100.32/0.0295C100.26/0.295D100.32/0.295 - Question 3 - Select One
Read the following list carefully ........ Neutrophils, erythrocytes, monocytes, macrophages, B iymphocyte , NK cells, T lymphocytes, thrombocytes.
How many of the above cells constitute cellular barrier of innate immunity ?AThreeBFourCFiveDSix
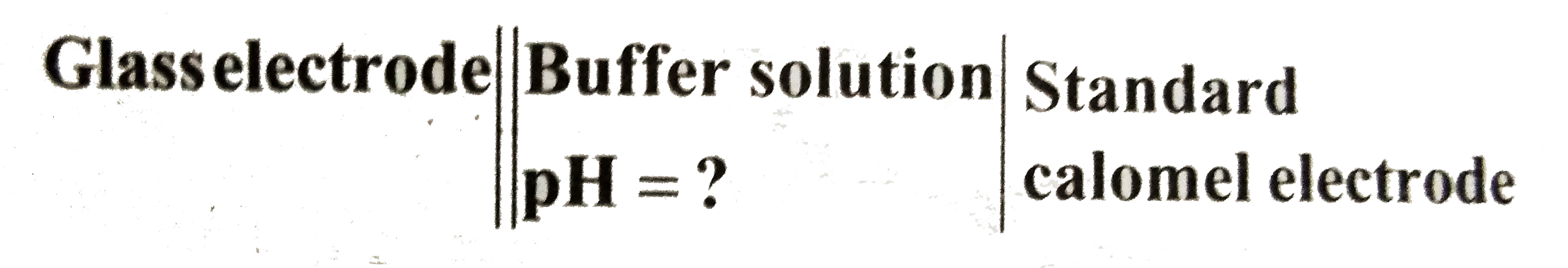
If the EMF of the above cell is 0.03V,ESCE=0.24V,Ec−.glass=0.51V, then calculate the pH of buffer solution at 30∘C.View SolutionZn∣∣Zn2+(a=0.1M)∣∣∣Fe2+(a=0.01M)Fe.
The EMF of the above cell is 0.2905. The equilibrium constant for the cell reaction isView SolutionZn∣∣Zn2+(a=0.1M)∣∣∣∣Fe2+(a=0.01M)∣∣Fe
The emf of the above cell is 0.2905 V. Equilibrium constant for the cell reaction is:View SolutionThe overall reaction electrochemical cell at 298K.
Ag(s)|AgI(s)|I−(aq)∣∣∣∣Cl−(aq)∣∣Hg2Cl2∣∣Hg(l)∣Pt(s)
[Given: E∘Cl−|Hg2Cl2|Hg=0.26V.E∘Ag+∣Ag=0.8V.
Ksp(Agl)=10−16 and 2.303RTF=0.06]
E∘cell of the above cell is:View Solution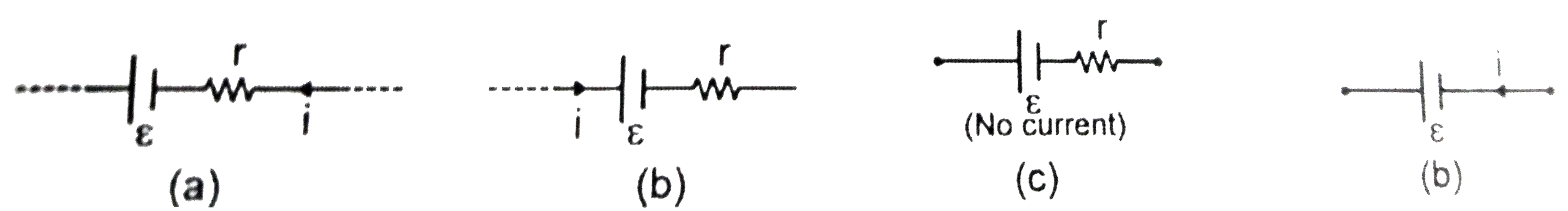
In which of the above cells, the potential difference between the terminals of a celll exceeds its emf.View Solution
