A solid sphere having uniform charge density ρ and radius R is shown in figure. A spherical cavity ofradius R2 is made in it. What is the potential at point O?

11R2p24ε0
5R2p12ε0
7pR212ε0
3R2p2ε0
The correct Answer is:B
Charge of whole sphere Q=(43πR3)p
Charge of the cavity q=43π(R2)2p=Q8, Now V0=[(Vv holesphere )-(V cavity)]
=38πe0QR=14πe0(QR)R2=516πe0QR,516πe0R×(43πR3p)=512R2pe0
Similar Questions
A solid sphere ofradius 'R' is uniformly charged with charge density ρin its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. It is given that ρR2∈0=48V. Find the electric potential at the centre C of the sphere:

View SolutionA Uniformly charged solid non-conducting sphere of uniform volume charge density ρ and radius R is having a concentric spherical cavity of radius r. Find out electric field intensity at following points, as shown in the figure :

(i) Point A (ii) Point B
(iii) Point C (iv) Centre of the sphere
View Solution
Knowledge Check
A solid sphere having radius R and uniform charge density ρ has a cavity of radius R2 as shown in figure.Find the value of ∣∣∣EAEB∣∣∣
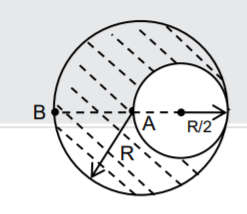 A1819B1117C917D919
A1819B1117C917D919A hemi-spherical cavity is created in solid sphere (of radius 2R) as shown in the figure. Then
 Axcm=−R/15Bycm=−R40Czcm=zeroDNone of these
Axcm=−R/15Bycm=−R40Czcm=zeroDNone of theseA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
A11GMmR2B14GMmR2CGMm2R2DGMmR2
A solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.

View SolutionA solid sphere having radius R and uniform charge density ρ has a cavity of radius R2 as shown in figure then the value of ∣∣∣(EAEB)∣∣∣=m17 .Find the value of m
View SolutionAn infinitely long solid cylinder of radius R with uniform volume charge density ρ has a spherical cavity of radius R2 with its centre on the axis of the cylinder as shown in the figure. The magnitude of the electric field at a point P which is at a distance 2R from the axis of the cylinder is given by 23ρR6Kε0. What is the value of K ?
View SolutionDistance between centres of two spheres A andB, each of radius R is r as shown in figure−1.450. SphereB has a spherical cavity of radius R/2 such that distance of centre of cavity is (r-R/2) from the centre of sphere A and R/2 from the centre of sphere B. Di-electric constant of material of each sphere is K = I and material of each sphere has a uniform charge density· p per unit volume. Calculate interaction energy of the two spheres :

View SolutionConsider a uniform charged sphere of charge density r and radius R.If the cavity of radius R/2is made inside the sphere and the removed part is again placed near the charge distribution as shown in the figure. If the electric field at the centre of the cavity is ρRnɛ0find n .
View Solution

