The perpendicular from the centre of a circle to a chord bisects the chord.
A perpendicular is drawn from the centre of a circle to the chord
To Find :
To prove that a perpendicular from the centre of a circle to a chord bisects the chord.
Solution :In triangle OAC and OBC,
∠OCA=∠OCB (both angles are90∘)
OA=OB (Radius of the circle)
OC=OC (common)
△OAC≅△OBC
AC=BC (Congruent parts of congruent triangles are equal)
Thus, C is the midpoint of the chord.
Therefore, the perpendicular drawn from the centre of a circle to a chord bisects the chord.
Hence proved.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The radius of a circle is 6 cm. The perpendicular distance from the centre of the circle to the chord which is 8 cm in length is
A√5 cmB2√5 cmC2√7 cmD√7 cmA 5 cm long perpendicular is drawn from the centre of a circle to a 24 cm long chord. Find the diameter of the circle.
AA) 26 cmBB) 32 cmCC) 13 cmDD) 30 cmThe straight line drawn from the centre of a circle perpendicular to a chord P–– the chord.
A straight line will not cut a circle in more than O–– distinct points.
R–– chords of a circle are equidistant from the centre of the circle.APQRTrisectThreePerpendicularBPQRDefinesTwoEqualCPQRBisectsTwoEqualDPQRBisectsThreeParallel
A line drawn drom the centre of a circle to a chord always bisects it. (True/False).
View SolutionThe radius of a circle is 10 cm and the perpendicular form the centre to a chord is 8cm. Find the length of the chord.
(ii) The radius of a circle is 10 cm. its one chord is 16 cm long. Find the perpendicular distance of this chord form the centre.
(iii) in the adjoining figure O is the centre of circle. the radius of circle is 17 cm . if OC=8cm, then find the length of chord AB.
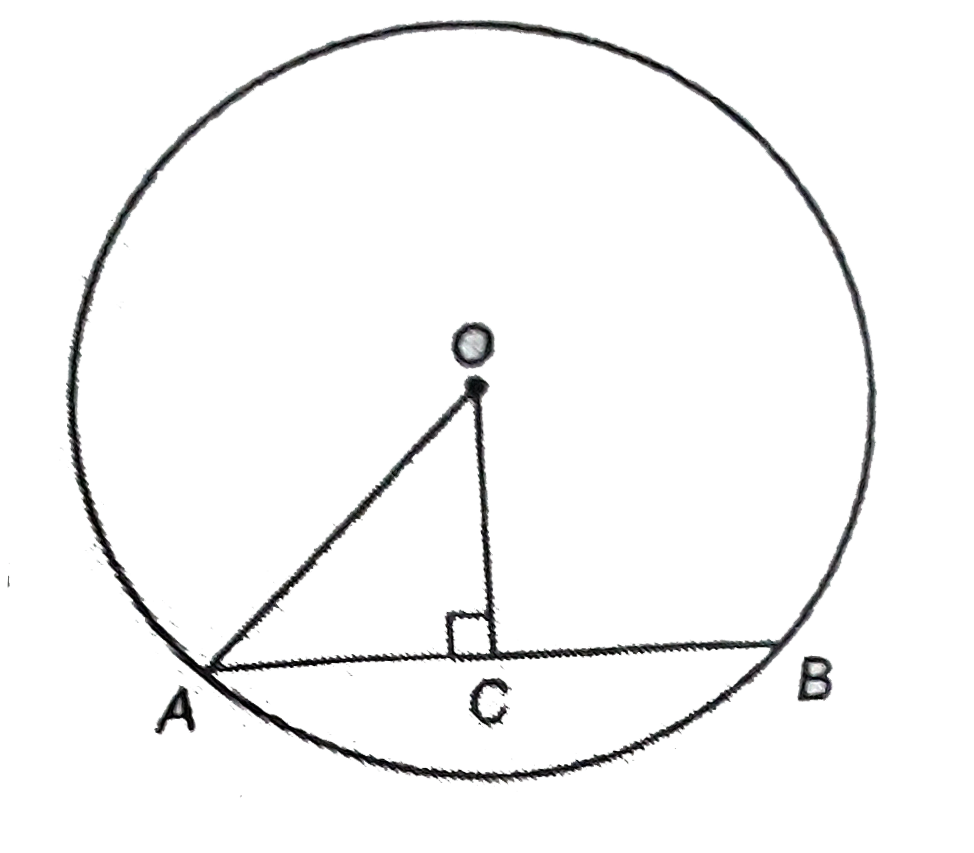
(iv) In the adjoining figure, OM⊥AB, radius OC=5cm and chord AB=8cm.Find the length of OM.
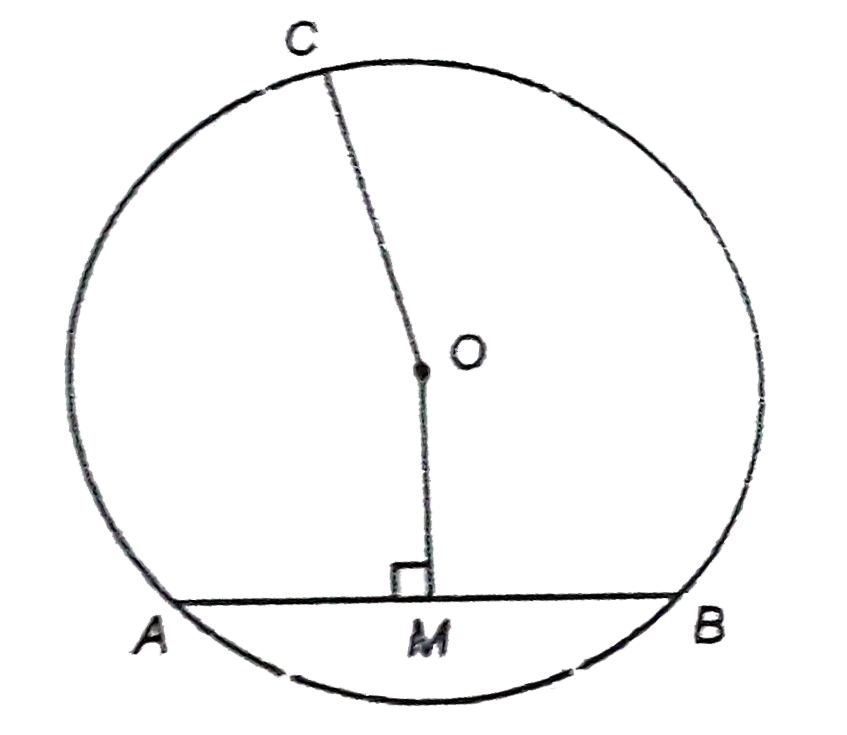
View SolutionTheorem 10.4 : The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.
View SolutionPS is the chord of the circle with centre O. A perpendicular is drawn from centre O of the circle to chord PS at M. If ¯¯¯¯¯PS=30cm and ¯¯¯¯¯¯¯OM=8cm, then find the radius of the circle.
View SolutionPS is the chord of the circle with centre O. A perpendicular is drawn from centre O of the circle to chord PS at M. If ¯¯¯¯¯PS=30cm and ¯¯¯¯¯¯¯OM=8cm, then find the radius of the circle.
View Solution
