In Figure, O is the centre of the circle of radius 5 cm.OP ⊥AB, OQ ⊥CD, ABCD, AB=6 cm and CD=8 cm. Determine PQ.
To solve the problem, we need to determine the length of segment PQ in the given circle configuration. Here’s a step-by-step solution:
Step 1: Understand the Problem
We have a circle with center O and radius 5 cm. Lines AB and CD are parallel, with OP perpendicular to AB and OQ perpendicular to CD. The lengths of AB and CD are given as 6 cm and 8 cm, respectively.
Step 2: Determine the Lengths of AP and CQ
Since OP is perpendicular to AB and bisects it, we can find AP and PB:
- AB=6 cm, so AP=PB=62=3 cm.
Similarly, since OQ is perpendicular to CD and bisects it, we can find CQ and QD:
- CD=8 cm, so CQ=QD=82=4 cm.
Step 3: Apply the Pythagorean Theorem
Now we will use the Pythagorean theorem to find OP and OQ.
For Triangle OAP:
- OA is the radius of the circle, which is 5 cm.
- AP=3 cm.
- We need to find OP.
Using the Pythagorean theorem:
OA2=OP2+AP2
52=OP2+32
25=OP2+9
OP2=25−9=16
OP=√16=4 cm
For Triangle OCQ:
- OC is also the radius of the circle, which is 5 cm.
- CQ=4 cm.
- We need to find OQ.
Using the Pythagorean theorem:
OC2=OQ2+CQ2
52=OQ2+42
25=OQ2+16
OQ2=25−16=9
OQ=√9=3 cm
Step 4: Calculate PQ
Now that we have OP and OQ, we can find PQ:
PQ=OP−OQ=4 cm−3 cm=1 cm
Final Answer
The length of PQ is 1 cm.
---
We have a circle with center O and radius 5 cm. Lines AB and CD are parallel, with OP perpendicular to AB and OQ perpendicular to CD. The lengths of AB and CD are given as 6 cm and 8 cm, respectively.
Since OP is perpendicular to AB and bisects it, we can find AP and PB:
- AB=6 cm, so AP=PB=62=3 cm.
- CD=8 cm, so CQ=QD=82=4 cm.
Now we will use the Pythagorean theorem to find OP and OQ.
- OA is the radius of the circle, which is 5 cm.
- AP=3 cm.
- We need to find OP.
OA2=OP2+AP2
52=OP2+32
25=OP2+9
OP2=25−9=16
OP=√16=4 cm
- OC is also the radius of the circle, which is 5 cm.
- CQ=4 cm.
- We need to find OQ.
OC2=OQ2+CQ2
52=OQ2+42
25=OQ2+16
OQ2=25−16=9
OQ=√9=3 cm
Now that we have OP and OQ, we can find PQ:
PQ=OP−OQ=4 cm−3 cm=1 cm
The length of PQ is 1 cm.
Topper's Solved these Questions
Similar Questions
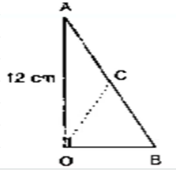
In Figure, ∠AOB=900, AC=BC, OA=12 cm and OC=6.5cm. Find the area of AOB.
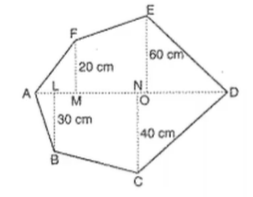
View SolutionFind the area of the following polygon, if AL=10cm, AM=20cm, AN=50cm, AO=60cm and AD=90cm.
View SolutionIn Figure, ABCD is a quadrilateral in which diagonal AC=84 cm ; DL⊥AC, BM⊥AC, DL=16.5 cm and BM=12 cm . Find the area of quadrilateral ABCD.
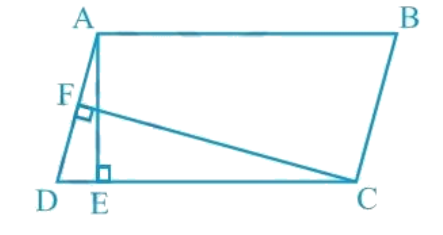
View SolutionIn Figure, ABCD is a parallelogram, AE ⊥DC and CF⊥AD . If AB=16CM, AE=8cm and CF=10cm, find AD
View SolutionAB and CD are two chords of a circle such that AB=6 cm, CD=12 cm and ABCD. If the distance between AB and CD is 3 cm, find the radius of the circle.
View SolutionIn Figure, ABCD is a rectangle with sides AB=10cmandAD=5cm Find the area of EFG
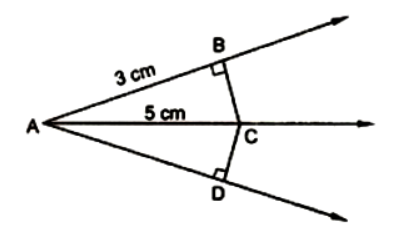
View SolutionIn Figure, if AC is bisector fo ∠BAD such that AB=3 cm and AC=5 cm, then CD= 2 cm (b) 3 cm (c) 4 cm (d) 5 cm
View SolutionIn a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC=21 cm, BC=29cm and AB=30cm, find the perimeter of the quadrilateral ARPQ
View SolutionIn Figure, M, N and P are the mid-points of AB, AC and BC respectively. If MN=3cm, NP=3.5cm and MP=2.5cm , calculate BC, AB and AC
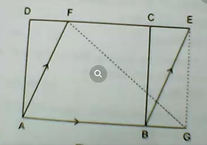
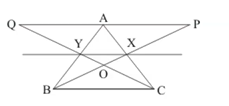
View SolutionIn Figure, XandY are the mid-points of ACandAB respectively, QP,BCandCYQandBXP are straight lines. Prove that ar(ABP)=ar(ACQ)
View Solution

