Question

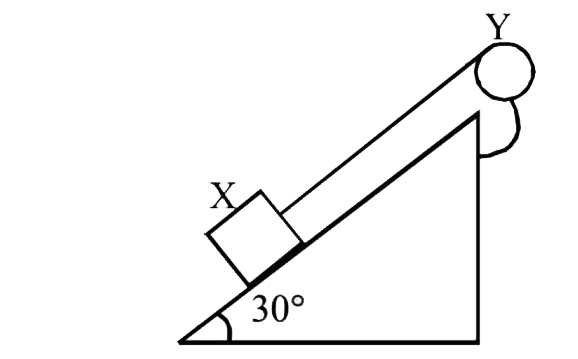
A block X of mass 0.5 kg is held by a long massless string on a frictionless inclined plane of inclination ${30}^{\circ }$ to the horizontal. The string is wound on a uniform solid cylindrical drum Y of mass 2kg and of radius 0.2 and of radius 0.2 m as shown in Fingure. The drum is given an initial angular velocity such that the block X starts moving up the plane.
(i) Find the tension in the string during the motion.
(ii) At a certain instant of time the magnitude of the angular velocity of Y s $10rad{s}^{-1}$ calculate the distance travelled by X from that instant of time until it comes to rest

Explanation

(i) `5//3`, (ii) `1.2`
(i) Force equation for the block is as follows:
`N=5 cos 30^(@) =0`…….(i)
`5 sin 30^(@) -T = 0.5 xx a`………(ii)

Torque equation for the drum,
`TR =(1/2 MR^(2))alpha`
`rArr T=1/2 MR.alpha =1/2 xx 2 xx 0.2 alpha rArr T=0.2 alpha`...........(iii)
Here, `a=R alpha`. (The string does not slip on the drum)
Thus, `T=(0.2)(a/R) =0.2 (a/0.2) = 1 xx a`........(iv)
From eqs. (ii) and (iv), we get `a=5/3m//s,T=5/3 N`
(ii) Angular velocity of Y=10 rad /s.
Velocity of block `X = Romega =0.2 xx 10 =m//s`, along the plane upwards.
Acceleration of `X=5//3 m//s^(2)` along the plane downwards.
Using equation `v^(2) =u^(2) -2as, 0^(2)=(2)^(2) -2 xx 5//3 xx s rArr s=(4 xx 3)/(2 xx 5) =1.2m`,