Question

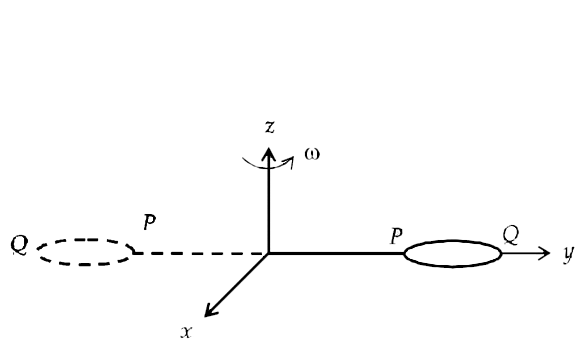
The general motion of a rigid body can be considered to be a combination of (i) a motion of its centre of mass about an axis, and (ii) its motion about an instantaneous exis passing through the centre of mass. These axes need not be stationary. Consider, for example, a thin uniform disc welded (rigidly fixed) horizontally at its rim to a massless, stick as shown in the figure. When the disc-stick system is rotated about the origin on a horizontal frictionless plane with angular speed ${\displaystyle \omega }$ the motion at any instant can be taken as a combination of (i) a rotation of the disc through an instantaneous vertical axis passing through its centre of mass (as is seen from the changed orientation of points P and Q). Both these motions have the same angular speed ${\displaystyle \omega }$ in this case

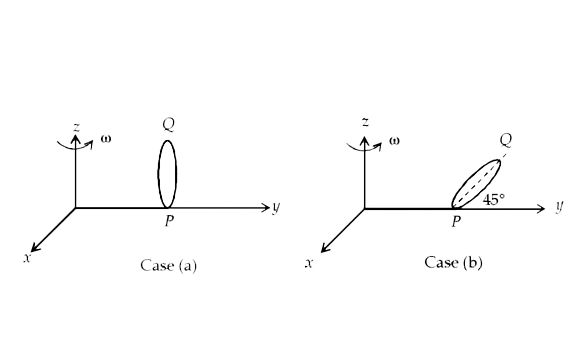
Now consider two similar system as shown in the figure: Case (a) the disc with its face vertical and parallel to x-z plane, Case (b) the disc with its face making an angle of ${\displaystyle {45}^{\circ }}$ with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point P, and the systems are rotated with constant angular speed ${\displaystyle \omega }$ about the z-axis.

Which of the following statements regarding the angular speed about the instantaneous axis (passing through the centre of mass) is correct?

Options

A. It is vertical for both the cases (a) and (b)
B. It is vertical for case (a) , and is at `45^(@)` to the x-z plane and lies in the plane of the disc for case (b)
C. It is horizontal for case (a) , and is at `45^(@)` to the x-z plane and is normal to the plane of the disc for case (b)
D. It is vertical for case (a) , and is at `45^(@)` to the x-z plane and is normal to the plane of the disc for case (b)

Answer

C

Explanation

Instantaneous axis passing through cm is vertical in both the cases