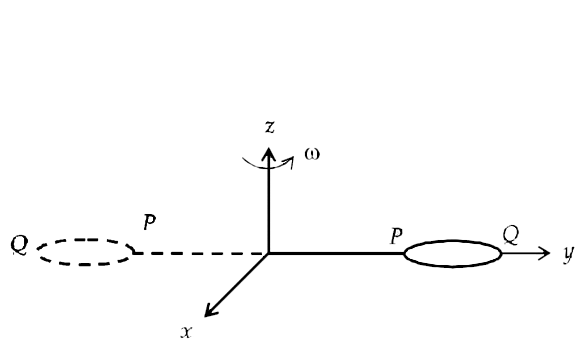
The general motion of a rigid body can be considered to be a combination of (i) a motion of its centre of mass about an axis, and (ii) its motion about an instantaneous exis passing through the centre of mass. These axes need not be stationary. Consider, for example, a thin uniform disc welded (rigidly fixed) horizontally at its rim to a massless, stick as shown in the figure. When the disc-stick system is rotated about the origin on a horizontal frictionless plane with angular speed ω the motion at any instant can be taken as a combination of (i) a rotation of the disc through an instantaneous vertical axis passing through its centre of mass (as is seen from the changed orientation of points P and Q). Both these motions have the same angular speed ω in this case
Now consider two similar system as shown in the figure: Case (a) the disc with its face vertical and parallel to x-z plane, Case (b) the disc with its face making an angle of 45∘ with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point P, and the systems are rotated with constant angular speed ω about the z-axis.
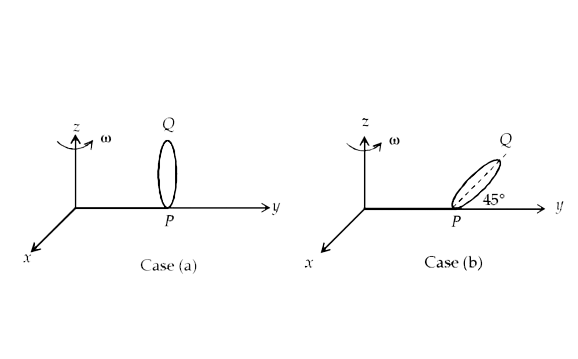
Which of the following statements regarding the angular speed about the instantaneous axis (passing through the centre of mass) is correct?
It is √2ω for both the cases
It is ω for case (a) , and ω√2 for case (b)
It is ω force case (a) , and √2ω for case (b)
If ω for both the cases.
The correct Answer is:D
Angular speed about the instantaneous axis passing through centre of mass is ω for both the cases.
Similar Questions
A horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
View SolutionA horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
View Solution
Knowledge Check
The radius of gyration of a uniform rod of length L about an axis passing through its centre of mass is
AL2√3BL212CL√3DL√2The radius of gyration of a uniform rod of length L about an axis passing through its centre of mass is
AL√12BL2√12CL√3DL√2Radius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
AR/√2BR/2C√2 RD2R
Calculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionRadius of gyration of a body about an axis at a distance 6 cm from its centre of mass is 10 cm. Find its radius of gyration about a parallel axis through its centre of mass.
View SolutionThe radius of gyration of an uniform rod of length L about an axis passing through its centre of mass and perpendicular to its length is.
View SolutionRadius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View Solution
