A slab is subjected to two forces →F1and→F2 of same magnitude F as shown in the figure . Force →F2 is in XY-plane while force F1 acts along z-axis at the point (2→I+3→j) .The moment of these forces about point O will be :

(3ˆi+2ˆj−3ˆk)F
(3ˆi−2ˆj−3ˆk)F
(3ˆi+2ˆj+3ˆk)F
(3ˆi−2ˆj+3ˆk)F
The correct Answer is:D
→τ1=(2ˆi+3ˆj)×(ˆk)F=(−2ˆj+3ˆi)F
→τ2=(6ˆj)×(F2)(−ˆi)=3Fˆk
So, →τ=(3ˆi−2ˆj+3ˆk)F

Similar Questions
Knowledge Check
Two forces −→F1and−→F2 are acting at right angles to each other , find their resultant ?
A√F21−F22B√F21+F22C√(F1+F2)DF1+F2If →F is the force acting in a particle having position vector →r and →τ be the torque of this force about the origin, then
A→r.→T=0 and →F.→T=0Bvec(r ) .vec(T) cancel(=) but →F.→T=0Cvec(r ) .vec(T) cancel(=) but vec(F).vec(T)cancel(=)0Dvec( r ) . vec( T )cancel( =) 0 and vec(F) .vec(T)cancel(=)0A force →F=3ˆi+2ˆj−4ˆk is applied at the point (1,−1,2). What is the moment of the force about the point (2,−1,3)?
Aˆi+4ˆj+4ˆkB2ˆi+ˆj+2ˆkC2ˆi−7ˆj−2ˆkD2ˆi+4ˆj+ˆk
A force →F=4ˆi+ˆk acts through point A (0, 2, 0). Find the moment →m of →F about the point B (4, 0, 4).
View SolutionIf →F is the force acting in a particle having position vector →r and →τ be the torque of this force about the origin, then
View SolutionA smooth track in the form of a quarter circle of radius 6m lies in the vertical plane. A particle moves from P1 to P2 under the action of forces →F1,→F2 and →F3 Force →F1 is 20N, Force →F2 is always 30N in magnitude. Force →F3 always acts tangentiallly to the track and is of magnitude 15N. Select the correct alternative (s) :
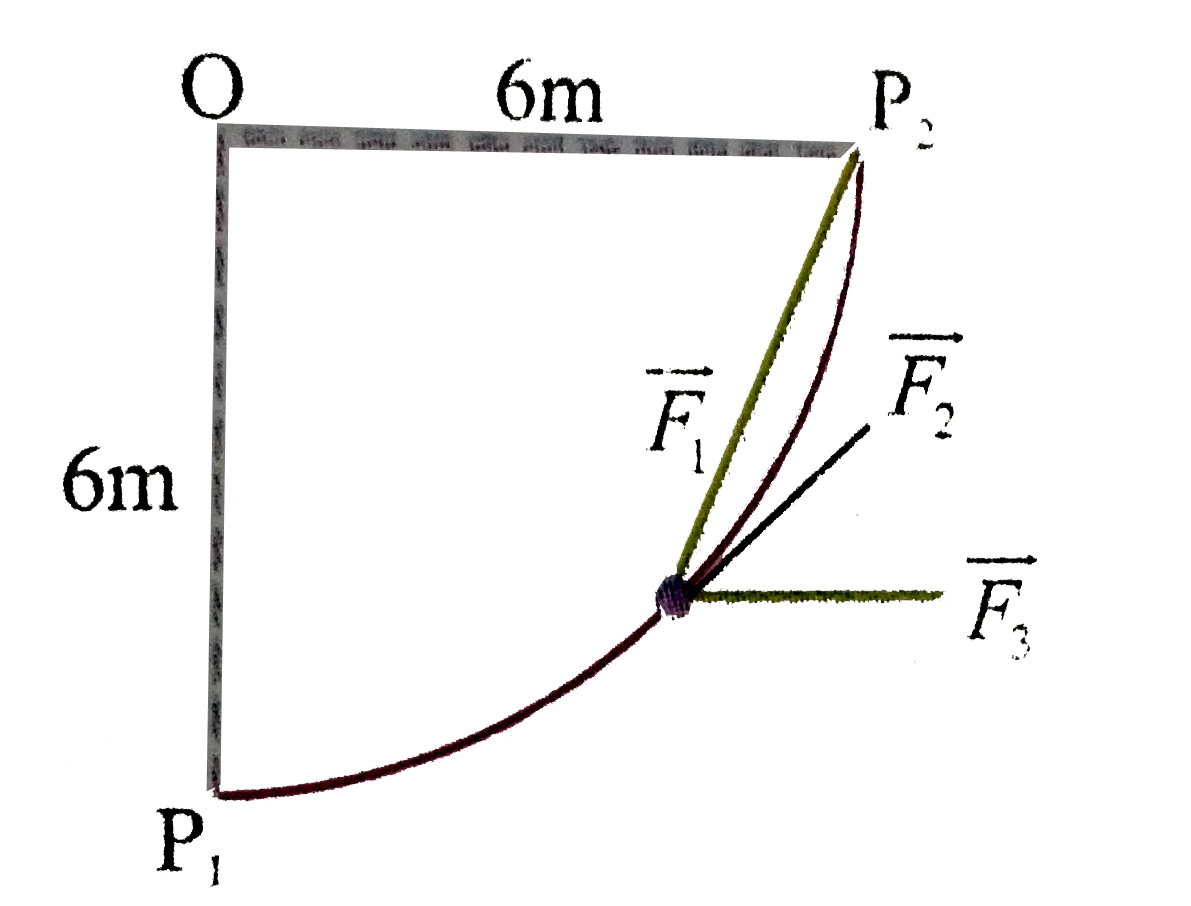 .
.
View SolutionTwo forces →F1=500N due east and →F2=250N due north have their common initial point. →F2−→F1 is
View SolutionA force →F1 of magnitude 9 N makes an angle of 30∘ with the X-axis. Another force →F2 of magnitude 12 N, makes an angle of 120∘ with the X-axis. What is the magnitude of the resultant force ?
View Solution