To mop-clean a floor, a cleaning machine presses a circular mop of radius R vertically down with a total force F and rotates it with a constant angular speed about its axis. If the force F is distributed uniformly over the mop and if coefficient of friction between the mop and the floor is μ the torque, applied by the machine on the mop is:
23μFR
μFR/3
μFR/2
μFR/6
The correct Answer is:A
dt=(df).x
=(μN)x
=μFπR2.2πxdx.x
=2μFR2x2dx
τ=2μF3R2R3=2μFR3

Similar Questions
To mop-clean a floor, a cleaning machine presses a circular mop of radius R vertically down with a total force F and rotates it with a constant angular speed about its axis. If the force F is distributed uniformly over the mop and the floor is μ, the torque, applied by the machine on the mop is :
View SolutionTo mop-clean a floor, a cleaning machine presses a circular mop of radius R vertically down with a total force F and rotates it with a constant angular speed about its axis. If the force F is distributed uniformly over the mop and the floor is μ, the torque, applied by the machine on the mop is :
View Solution
Knowledge Check
In Fig. 7.149 , coefficient of friction between the block and the floor is μ . Force F that will move the block on the floor with a uniform speed is :
 A(μsinθ+cosθ)mgB(μsinθ−cosθ) mgCμmgcosθ−μsinθDμmgsinθ−μcosθ
A(μsinθ+cosθ)mgB(μsinθ−cosθ) mgCμmgcosθ−μsinθDμmgsinθ−μcosθYou want to apply a force on a box so that it moves with constant speed across a horizontal floor. The coefficient if kinetic friction between the box and the floor is μk. Of the flur following cases, the force you apply on the box will be smallest when you
Apush it with a force applied horizontally at an angle 0<θ<90∘ in downword direction.Bpull it with a force applied horizontally at the same angle as in (A), in upward direction.Cdo either (A) or (B) since the applied force is the same.Dpush or pull with a force applied horizontally.A horizontal force F pulls a 20 kg box at a constant speed along a horizontal floor. If the coefficient of friction between the box and the floor is 0.25,how much work is done by the force F in moving the box through a distance of 2 m?
A49JB98JC147JD196J
A uniform solid cylinder of mass m rests on two horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F.
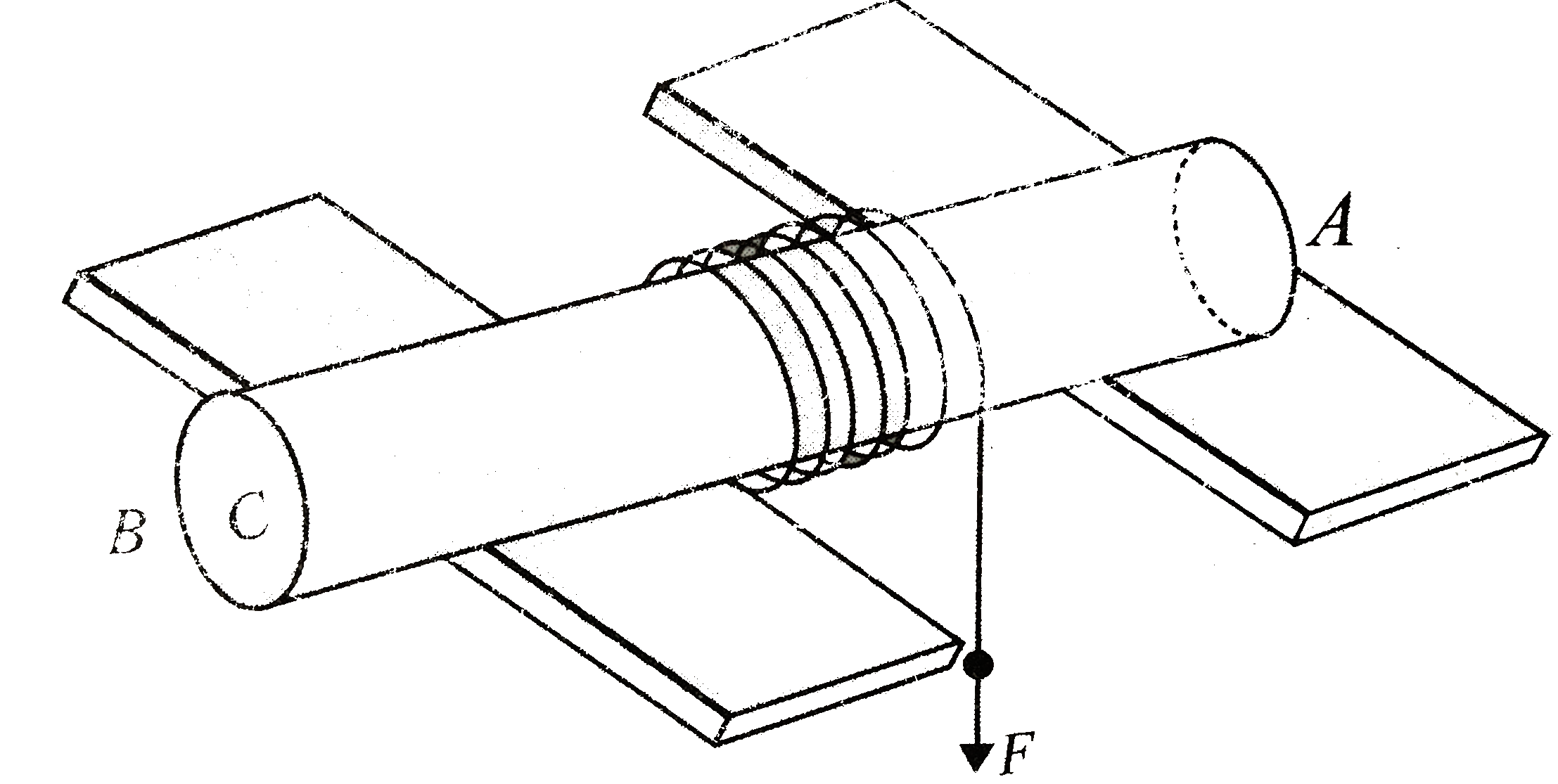
Find the maximum magnitude of the force F which may be applied without bringing about any sliding of the cylinder, if the coefficient of friction between the plank and the cylinder is equal to μ. What is the maximum acceleration of the centre of mass over the planks?
View SolutionA disc of radius R rotates from rest about a vertical axis with a constant angular acceleration such that a coin placed with a tangenitial between a as shown in figure If the coefficient of static friction between the coin and disc is μs .Find the velocity of the before it start sliding relative as the disc

View SolutionA hollow sphere of radius r is rotating about a horizontal axis at some angular speed ω0. It is gently lowered to ground and the coefficient of friction between sphere and the ground is μ.How far does the sphere move before it starts pure rolling?
View SolutionA uniform solid cylinder of mass m rests on two horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F(figure).
Find the maximum magnitude of the force F which still does not bring about any sliding of the cylinder, if the coefficient of friction between the cylinder and the planks is equal to k. What is the acceleration wmax of the axis of the cylinder rolling down the inclined plane?

View SolutionA horizontal force F pulls a 20 kg box at a constant speed along a rough horizotal floor. The coefficient of friction between the box and the floor is 0.25. The work done by force F on the block in displacing it by 2 m is
View Solution
