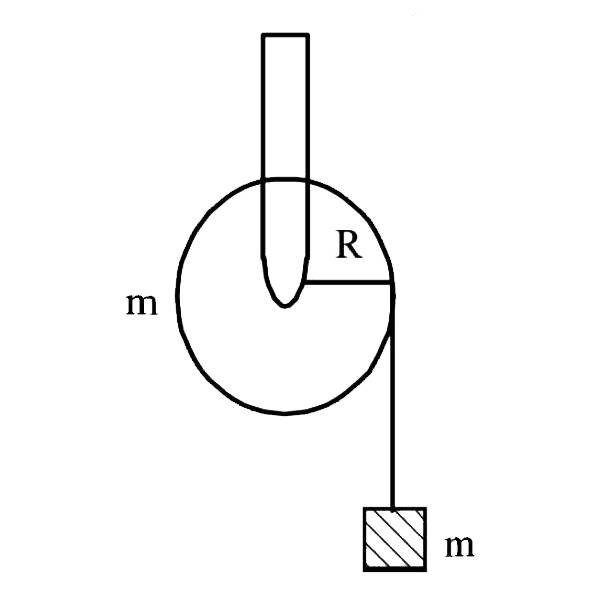
A mass 'm' is supported by a massless string wound around a uniform hollow cylinder of mass m and radius R. If the string does not slip on the cylinder, with what acceleration will the mass fall or release?
A mass 'm' is supported by a massless string wound around a uniform hollow cylinder of mass m and radius R. If the string does not slip on the cylinder, with what acceleration will the mass fall or release?

A

2 g 3

B

g 2

C

5 g 6

D

g

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B

For the mass m, mg - T = ma
As we know, a = R α
So, m g - T = m R α ……(i)
As torque = T × R = m R 2 α ……..(ii)
From Eqs. (i) and (ii), we get a = g / 2
ocr_image
Hence, the body will fall with an acceleration g 2 .

Updated on:21/07/2023
|
Class 12PHYSICSROTATIONAL MOTION

Similar Questions

Knowledge Check

  • A mass M is supported by a massless string wound round a uniform cylinder ofmass M and radius R. On releasing the mass from rest, it will fall with acceleration?
    ocr_image

    Ag
    Bg/2
    Cg/3
    D2g/3

  • A rope is wound round a hollow cylinder of mass M and radius R. If the rope is pulled with a force F newton, then the angular acceleration of the cylinder will be

    AMRF
    BMRF
    CRMF
    DFMR

  • A rope is wound round a hollow cylinder of mass M and radius R. If the rope is pulled with a force F newton, then the angular acceleration of the cylinder will be

    AF/MR
    BM/F R
    CR/MF
    DMR/F