A block of mass m is attached to a pulley disc of equal mass, radius r by means of a slack string as shown. The pulley is hinged about its centre on a horizontal table and the block is projected with an initial velocity of 5m/s. Find the velocity when the string becomes taut.
 .
.
3 m/s
2.5 m/s
5/3 m/s
10/3 m/s
The correct Answer is:D
Let J: impulse generated in the string ⇒J=12mr2ω….. For pulley
For block, −J=mv2−mv…. And v2=rω
where v2 is velocity of the block just after the string becomes taut.
⇒0=mv22+mv2−mv⇒v2=2v3=10/3m/s
Similar Questions
Two blocks A and B are joined by means of a slacked string passing over a massless pulley as shown in Figure. The system is released from rest and it becomes taut when B falls a distance 0.5m.
a. Find the common velocity of the two blocks just after the string becomes taut.
b. Find the magnitude of impulse on the pulley by the clamp during the small interval while string becomes taut.

View SolutionA block is connected to a disc pulley of same mass m radius R. If the acceleration of the block is 2gZ , find Z.
View Solution
Knowledge Check
A block of mass m is attached to one end of a light string which is wrapped on a disc of mass 2m and radius R. The total length of the slack portion of the string is 1. The block is released from rest. The angular velocity of the disc just after the string becomes taut is
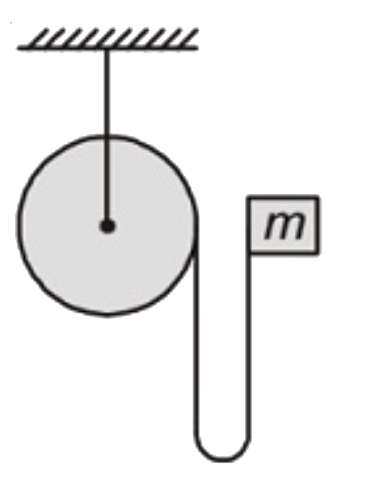 A√glR3B√gl2R2C√2gl3R2D√3gl2R2
A√glR3B√gl2R2C√2gl3R2D√3gl2R2A uniform cubical block of mass M is attached to a pulley. One end of a string, passing over the pulley is fixed to a light pole while is fixed on the bigger block and its another end is attached to a block of mass m as shown in figure. The maximum value of the mass m so that the block does not topple is : (string and pulley are ideal)
 AMl1(l2−l1)B2Ml1(l2−l1)CMl12(l2−l1)DM(l1+l2)2l1
AMl1(l2−l1)B2Ml1(l2−l1)CMl12(l2−l1)DM(l1+l2)2l1Two bodies of masses m and M are attached to the two ends of a light string passing over a fixed ideal pulley (M>>m). When the bodies are in motion, the tension in the string is approximately
A(m−m)gBmgC2mgD(mM)mg
A block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string passing over a smooth pulley. The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m
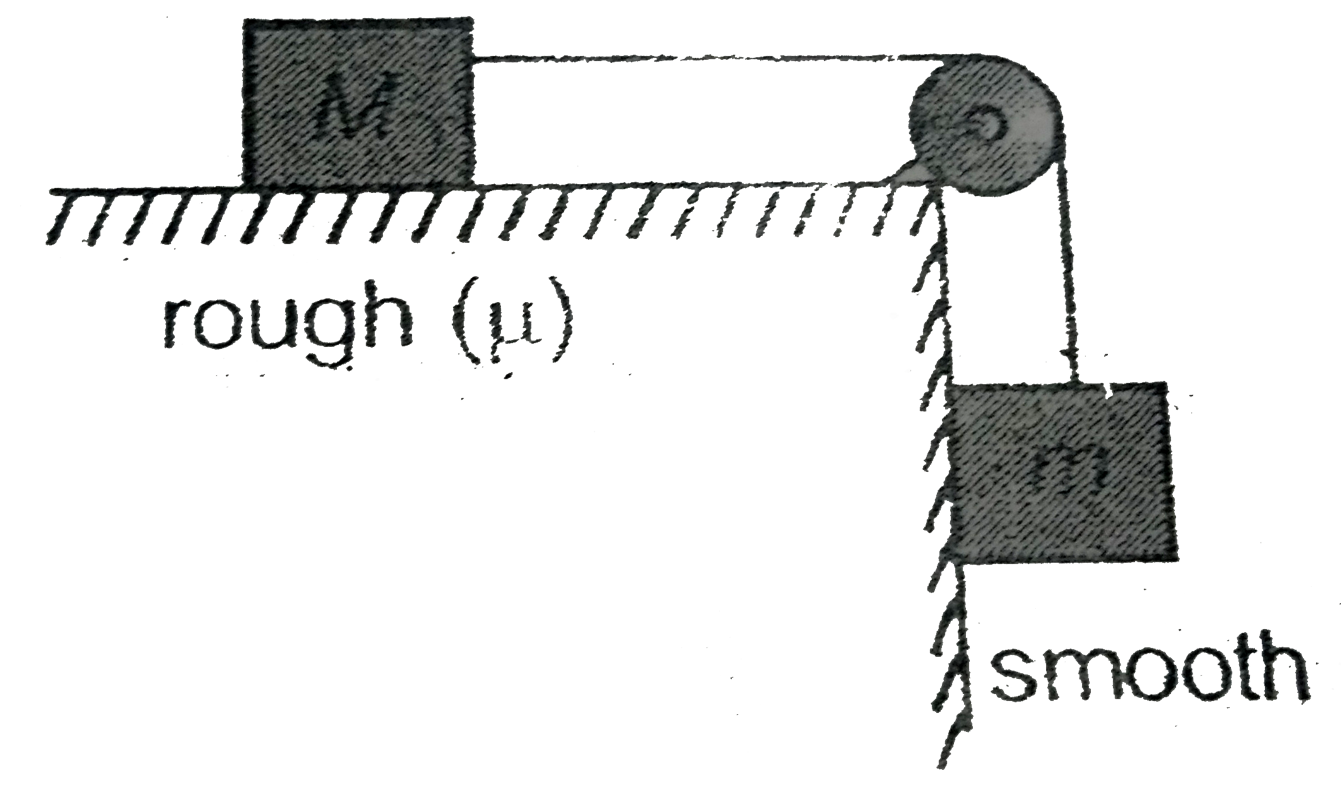
If the whole system ( horizontal surface + blocks ) accelerates towards right the value of maximum on the horizontal surface is
View SolutionA particle A of mass 2m is held on a smooth horizontal table and is attached to one end of an inelastic string which runs over a smooth light pulley at the edge of the table. At the other end of the string there hangs another particle B of mass m, the distance from A to the pulley is l. The particle A is then projected towards the pulley with velocity u.

(a) Find the time before the string becomes taut, and shown that after the string becomes taut, the initial velocity of A and B is 4u/3.
(b) Find the common velocity when A reaches the pulley (assume that B has not yet reached the ground).
View SolutionA block of mass m hangs by means of a string which goes over a pulley of mass m and moment of inertia l, as shown in the diagram. The string does not relative to the pulley. Find the frequency of small oscillations.
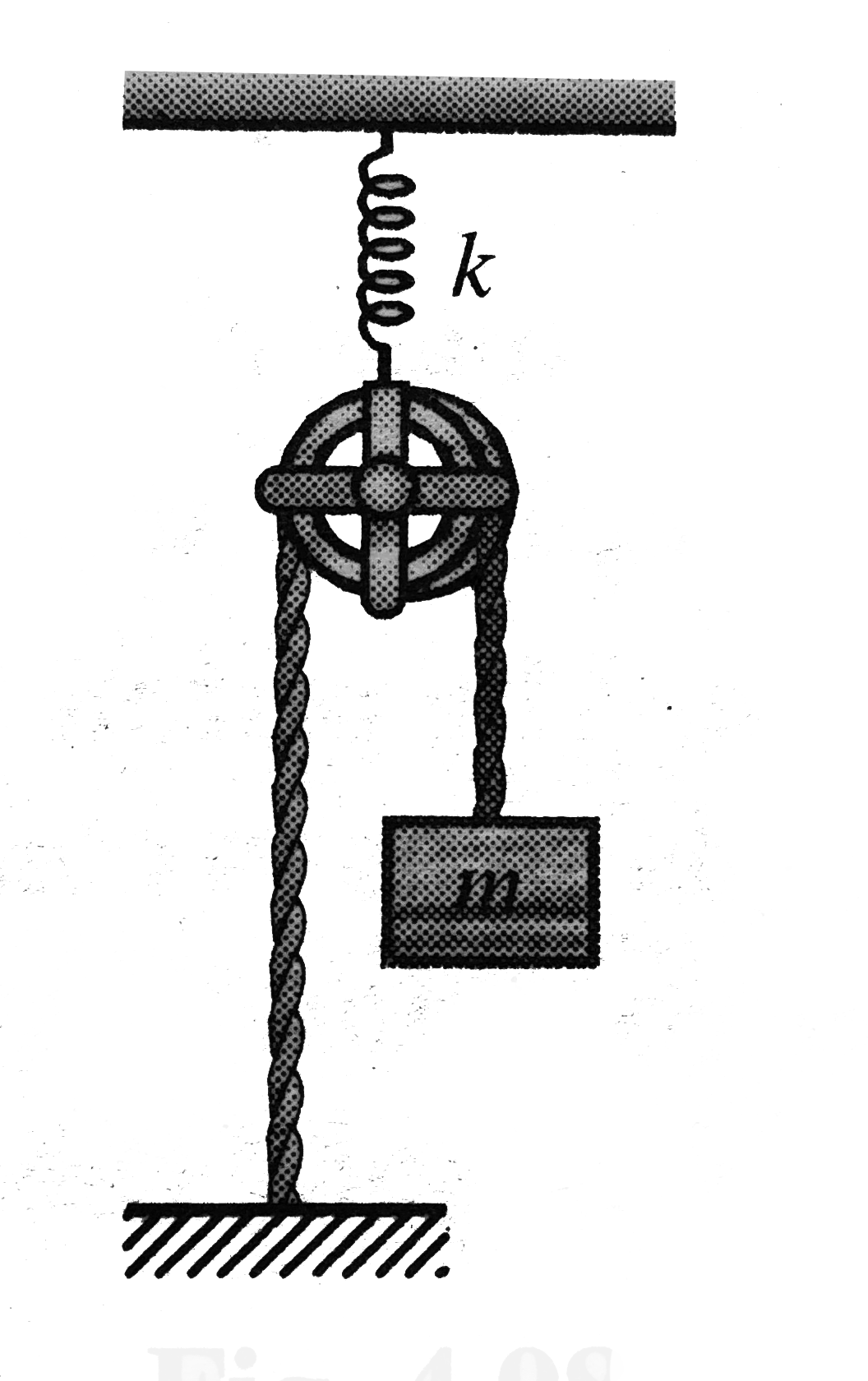
View SolutionTwo blocks A and B are joined by means of a slacked string passing over a massiess pulley as shown in diagam. The system is released from rest and it becouse taut when B falls a distance 0.5 m, then
(a) find the common velcoity of two blocks just after string become taut.
(b) Find the magnitude of impulse on the pulley by tyhe clamp during the small interval while string becomes taut

View SolutionA string of negligible mass is wrapped on a cylindrical pulley of mass M and radius R. The other end of string is tied to a bucket of mass m. If the pulley rotates about a horizontal axis then the tension in the string is :
View Solution
