A stepped cylinder having mass 50kg and a radius of gyration (K) of 0.30m. The radii R1 and R2 are respectively 0.3m and 0.6m. A pull T equal to 200N is exerted on the rope attached to inner cylinder. The coefficient of static and dynamic friction between cylinder and ground are 0.1 and 0.08 respectively.
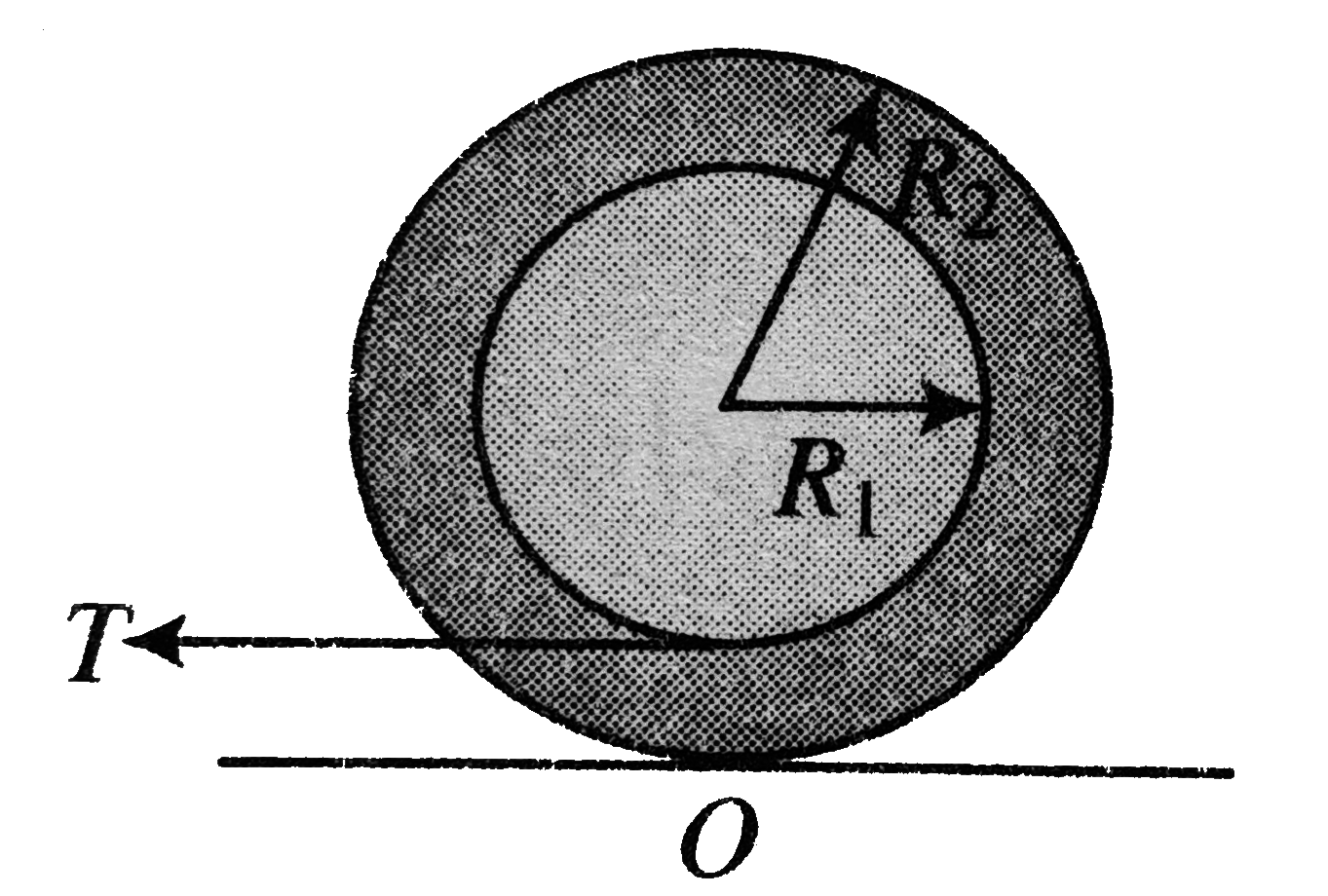
The angular acceleration is 2.67 radii s2
The force of kinetic friction is 40N
The acceleration is −3.2pm/s2
None of the above
The correct Answer is:B, C
Let F is the force applied to the rope and assuming the cylinder rolls without siding.

⇒F−f=ma⇒a=(f(1−R1/R2)m(1+R2/R22))
fR2−FR1=mk2α
a=R2α
N=mg & f=F[K2+R1R2]K2+R22
And to avoid sliding f≤Nμ
⇒F[R2+R1R2]K2+R22≤mgμs⇒F≤mgμS[R2+R22]K2+R1R2
⇒F≤50×10×0.10.32+0.620.32+(0.3)(0.6)⇒F≤2503N
But applied force is 200 N ⇒ rolling with sliding and f=fg=NμK=50×10×0.08=40N
a=F−fm towards left =20−4050=3.2m/s2
Similar Questions
A thin but very large plank of mass 2 m is placed on a horziontal smooth surface. A solid cylinder of mass m and radius r is given only translational velocity v0 and gently placed on the plank as shown in the figure. The coefficient of kinetic friciton between the plank and the cylinder is μ.

View SolutionIn Fig. 6-37, a block of mass m = 5.0 kg is at rest on a ramp. The coefficient of static friction between the block and ramp is not known. Find the magnitude of the net force exerted by the ramp on the block.

View Solution
Knowledge Check
A solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
Africtional force is always μmgcosθBfriction is a dissipative forceCby decreasing θ, frictional force decreasesDfrictiona opposes translation and supports rotation.A solid cylinder of radius 0.5 m and mass 50 kg is rotating at 300 rpm. Then the torque which will bring it to rest in 5 seconds is
A25πNmB25π2NmC50πNmD100πNmA soild cylinder of mass 2 kg and radius 0.2 m is rotating about its owm axis without friction with an angular velocity of 3 rad s−1 . Angular momentum of the cylinder is
A0.2 J sB1.12 J sC0.12 J sD12 J s
A cylinder of mass M = 2 kg and radius R = 12 cm lies on a plank of the same mass as shown in the figure. The surface between plank and ground is smooth but there is friction between cylinder and plank. If the coefficient of friction between the cylinder and the plank is μ=0.4, then what maximum initial compression (in cm) can be given to the spring such that the cylinder moves without slipping with respect to the plank ? [Given, k=200 N m−1]
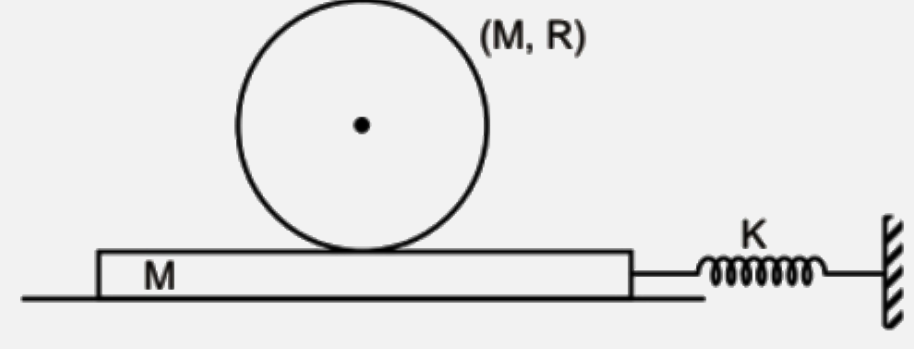
View Solution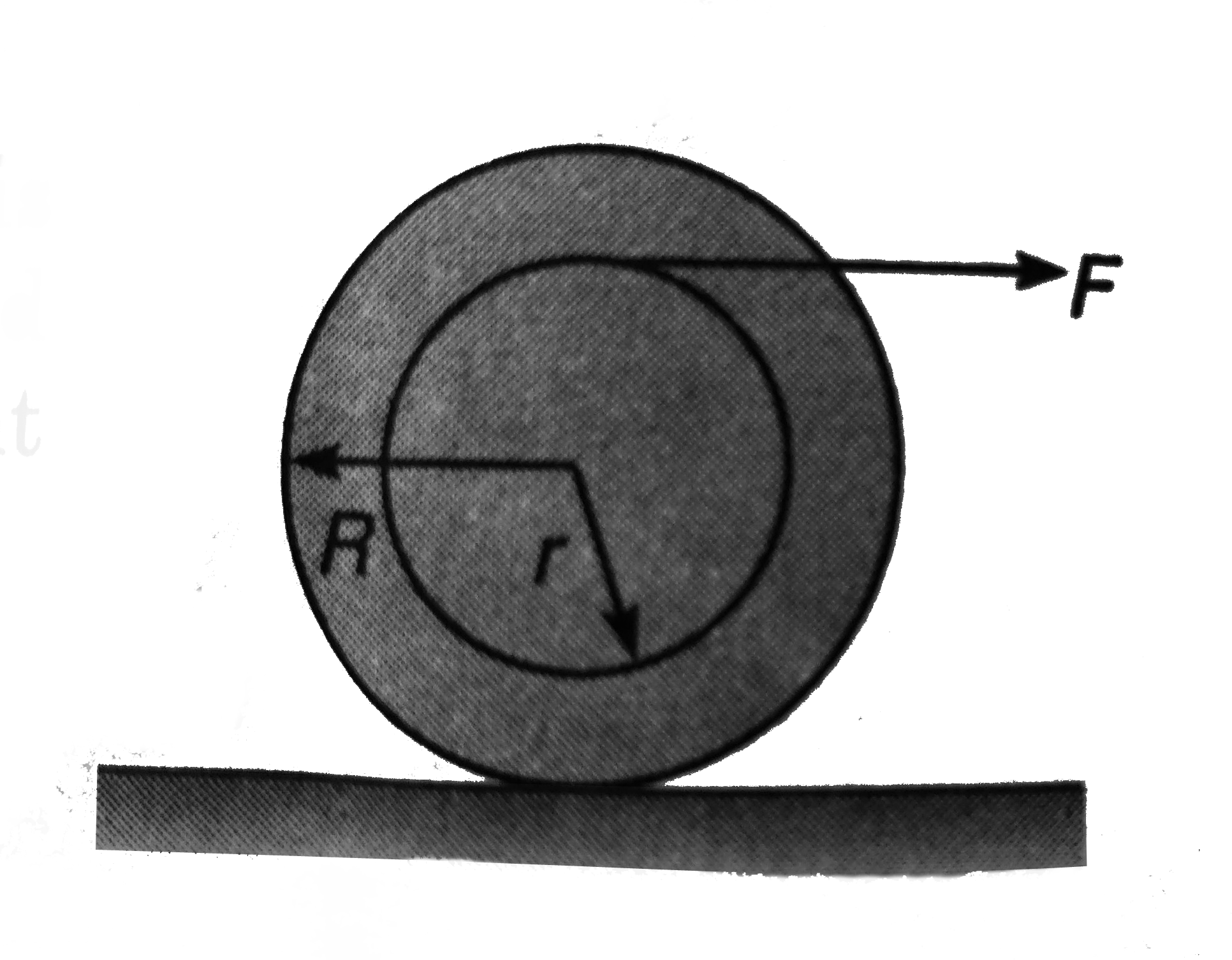
A heavy homogeneous cyliner has mass m and radius R. It is accelerated by a force F which is applied through a rope wound around a light drum of radius r attached to the cylinder (figure) the coefficient of static friction is sufficient for the cylinder to roll without slipping.
View SolutionA cylinder of 10 kg is sliding in a plane with an initial velocity of 10 m / s . If the coefficient of friction between the surface and cylinder is 0.5 then before stopping, it will cover. (g=10m/s2)
View SolutionA solid cylinder of mass 20 kg has length 1 m and radius 0.2 m. Then its moment of inertia (in kg m ) about its geometrical axis is (in kg m2)
View SolutionA solid cylinder of mass 1 kg and radius 0.02 m, is rolling on a smooth horizontal surface with a uniform velocity of 0.1 m/s. Its total energy is
View Solution
