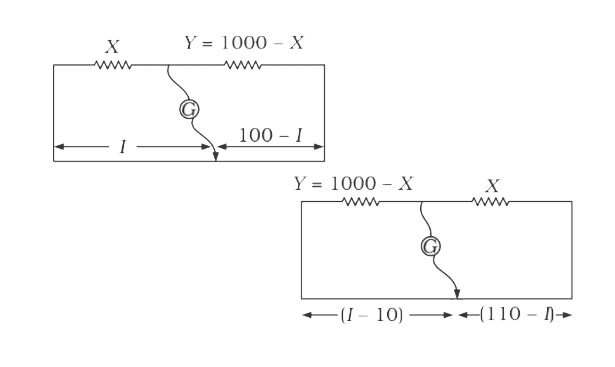
On interchanging the resistances, the balance point of a meter bridge shifts to the left by 10 cm. The resistance of their series combination is $1 k Ω$ . How much was the resistance on the left slot before interchanging the resistances ?

$990 Ω$

$505 Ω$

$550 Ω$

$910 Ω$

Video Solution

Text Solution

Verified by Experts

We have $X + Y = 1000 Ω$
Initially $\frac{X}{I} = \frac{1000 - X}{100 - I}$ ……..(i)
When X and Y are intercharged then $\frac{1000 - x}{I - 10} = \frac{X}{100 - (I - 10)}$
or $\frac{1000 - X}{I - 10} = \frac{X}{110 - I} \dots . (i i)$
From Eqs. (i) and (ii), we get
$\frac{100 - I}{I} = \frac{I - 10}{110 - I}$
$(100 - I) (110 - I) = (I - 10) I$
$11000 - 100 I - 100 + I^{2} = I^{2} - 10 I \Rightarrow 11000 = 200 I$
$∴ I = 55 c m$
Substituting the value of I in Eq (i) we get
$\frac{X}{55} = \frac{1000 - 55}{100 - 55} \Rightarrow 20 X = 11000 ∴ X = 550 Ω$

Updated on:21/07/2023

Two equal resistances are introduced in two gaps of a metre bridge. The shift in the null point if an equal resistance is connected in series with resistance in left gap is
A16.6 cm
B16.6m
C16.6mm
D66.6 cm
The points in a metre bridge is at 35.6 cm. if the resistances in the gaps are interchanged, the new balance point is
A64.4 cm
B56 cm
C41.2 cm
D56.7 cm
In a metre bridge expt, when the resistances in the gaps are interchanged the balance point is increases by 10 cm. The ratio of the resistances is
A $\frac{15}{5}$
B $\frac{12}{8}$
C $\frac{11}{9}$
D $\frac{10}{9}$