Twelve resistors of equal value R are connected in the form of a cube. Effective resistance between diagonals of the cube is

125R
56R
79R
116R
To redraw circuit, we join resistors across points which are same potentials. This can be judged on the basis of symmetry of circuit.

Req=R3+R6+R3=2R+R+2R6
=5R6Ω
Similar Questions
Twelve wires of equal length and same cross-section are connected in the form of a cube. If the resistance of each of the wires is R, and the effective resistance between the two diagonal ends is Re, then the ratio RRe is equal to __.
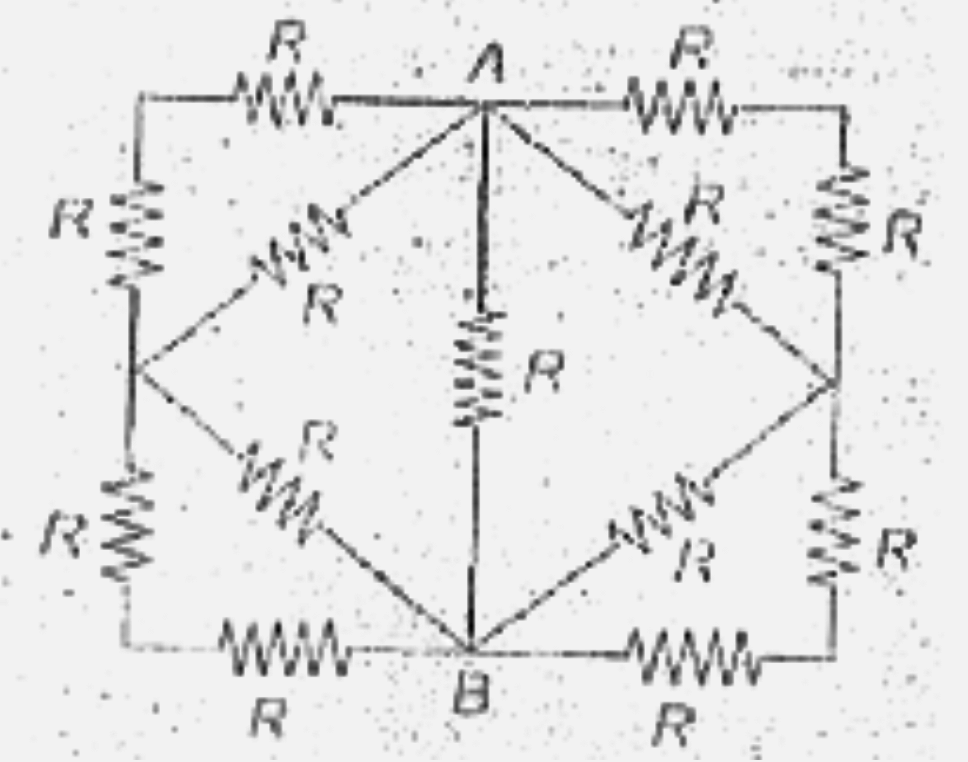
View SolutionThirteen resistors each of resistance R are connected in the circuit as shown . The effective resistance between A and B is
View Solution
Knowledge Check
The angle between two diagonals of a cube İs
Acos−1(13)B30∘Ccos−1(1√3)D45∘The angle between two diagonals of a cube will be
Asin−1(13)Bcos−1(13)CvariableDnone of theseThe angle between two diagonals of a cube will be
Asin−1(13)Bcos−1(13)CvariableDnone of these
The cosine of the angle between any two diagonals of a cube is
View SolutionFind the angel between any two diagonals of a cube.
View SolutionTwelve wires, each of resistance 6Ω are connected to form a cube. The effective resistance between two diagonally opposite corners of the cube is
View SolutionTwelve wires of equal length and same cross-section are connected in the form of a cube. If the resistance of each of the wires is R , then the effective resistance between the two diagonal ends would be

View SolutionFour wires of equal length and of resistance 5ohm each are connected in the form of a square. The equivalent resistance between the diagonally opposite corners of the square is
View Solution