Three vectors →A,→B and →C add up to zero.Find which is false.
(A×B)×C is not zero unless B, C are parallel
(A×B).C is not zero unless B, C are parallel
If A, B, C define a plane, (A×B)×C is in that plane
(A×B).C=|A||B||C|→C2=A2+B2
The correct Answer is:B, D
Given A+B+C=0
Hence, we can say that A, B and C are in one plane and are represented by the three sides of a triangle taken in one order, Now consider the options one by one.
(a) We can write
B×(A+B+C)=B×0=0
⇒ B×A+B×B+B×C=0
⇒ B×A+0+B×C=0
⇒ B×A=−B×C
⇒ A×B=B×C
∴ (A×B)×C=(B×C)×C
It cannot be zero.
If B||C, then B×C=0, than (B×C)×C=0.
(b) (A×B).C=(B×AC).C=0 whatever be the positions of A, B and C. If B||C, then B×C=0, then (B×C)×C=0.
(c) (A×B)=X=ABsinθX. The direction of X is perpendicular to the plane containing A and B. (A×B)×C=X×C. Its direction is in the plane of A, B, and C.
(d) If C2=A2+B2, then angle between A and B is 90∘
∴ (A×B).C=(AB sin90∘ X).C=AB (X.C)
ABCcos90∘=0
Topper's Solved these Questions
Similar Questions
Three vectors →A,→B and →C are such that →A=→B+→C and their magnitudes are in ratio 5:4:3 respectively. Find angle between vector →A and →C
View SolutionConsider three vectors →A,→Band→C as shown in fig. perform graphically the following vector additions and subtractions (a) →A+→B
(b). →A+→B+→C
(c). →A−→B
(d). →A+→B−→C

View Solution
Knowledge Check
In a righht angled triangle the three vectors →a,→b and →c add to zero. Then →a,→b is
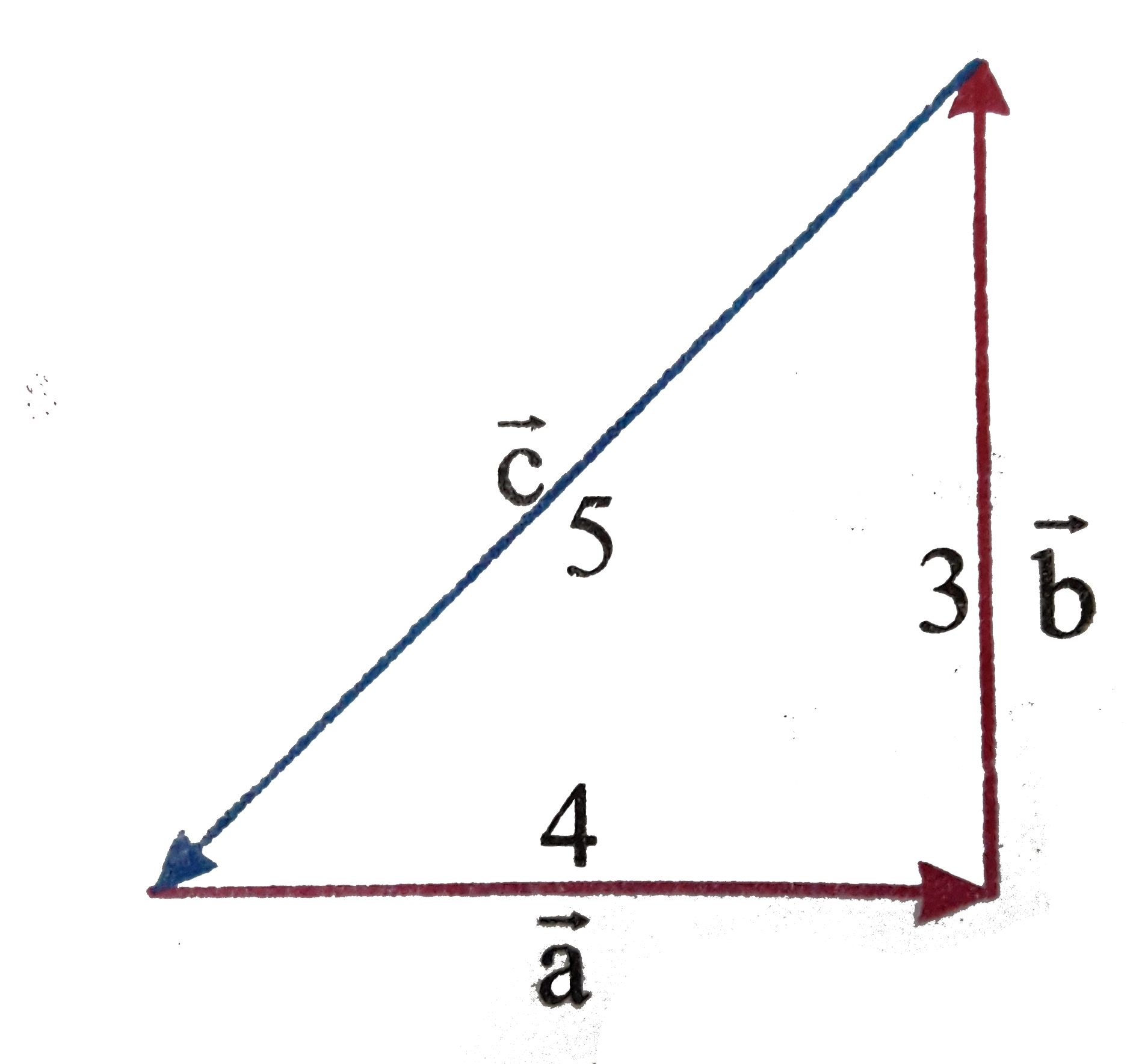 A−9B+9C0D−3
A−9B+9C0D−3The vector sum of three vectors→A,→B and →C is zero . If ˆi and ˆj are the unit vectores in the vectors in the directions of →A and →B respectively , them :
A→C is in the plane of ˆi of ˆjB→C is along ˆi׈jC→C is along ˆiD→C is alongˆjThree vectors →A,→B and →C satisfy the relation →A.→B=0 and →A.→C=0. The vector →A is parallel to
A→BB→CC→B.→CD→B×→C
Three vectors →A,→B,→C are shown in the figure. Find angle between
(i) →A and →B (ii) →B and →C (iii) →A and →C.
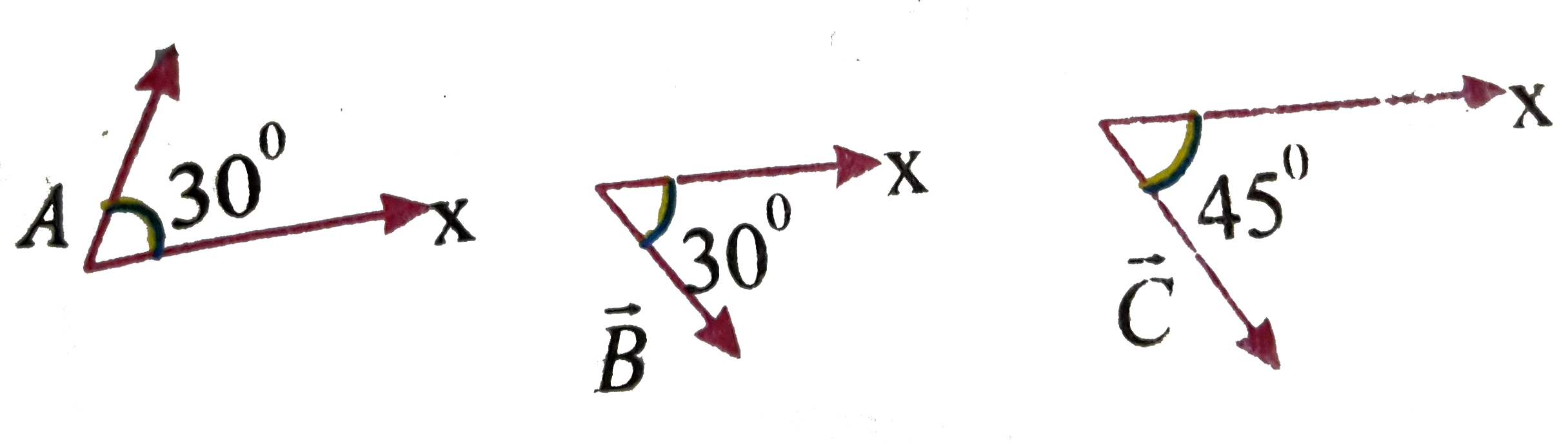
View SolutionGiven three vectors e→a,→band→c two of which are non-collinear. Futrther if (→a+→b) is collinear with →c,(→b+→c) is collinear with →a,|→a|=∣∣→b∣∣=|→c|=√2 find the value of →a.→b+→b.→c+→c.→a
View SolutionGiven three vectors →a,→b and →c are non-zero and non-coplanar vectors. Then which of the following are coplanar.
View SolutionIf three vectors →A,→Band→C satisfy the relation →A.→B=0&→A.→C=0 then the vector →A is parallel to →B×→C.
Statement-2 : →A⊥→B and →A⊥→C hence A is perpendicular to plane formed by →Band→C.
View SolutionThree vectors →a,→b and →c satisfy the relation →a.→b=0 and →a.→c=0. The vector →a is parallel to
View Solution
