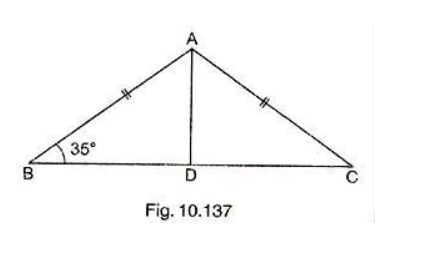
In an isosceles triangle altitude from the vertex bisects the base. GIVEN : An isosceles triangle ABC such that AB=AC and an altitude AD from A on side BC. TO PROVE : D bisects BC i.e. BD=DC. Figure
Given- AB=AC
TO prove= BD=CD
Proof-In∠ADBand∠ACD
∠ADB=∠ADC(each 90)
AD=AD(common)
∠B=∠C
∠ADB≅∠ACD(AAS)
BD=CD.
Topper's Solved these Questions
Similar Questions
In an Isoceless triangle altitude from the vertex bisects the base.
View SolutionIn an isosceles triangle altitude from the vertex bisects the base. GIVEN : An isosceles triangle ABC such that AB=AC and an altitude AD from A on side BC. TO PROVE : D bisects BC i.e. BD=DC. Figure
View SolutionThe altitude from the vertex bisect the base in an isosceles triangle
View SolutionIf ΔABC is an isosceles triangle such that AB=AC, then altitude AD from A on BC bisects BC (Fig.43).
View SolutionIf ABC is an isosceles triangle such that AB=AC and AD is an altitude from A on BC . Prove that (i) ∠B=∠C (ii) AD bisects BC (iii) AD bisects ∠A
View SolutionIf the altitude from one vertex of a triangle bisects the opposite side, then the triangle is isosceles. GIVEN : A ABC such that the altitude AD from A on the opposite side BC bisects BC i.e., BD=DC. TO PROVE : AB=AC i.e. the triangle ABC is isosceles.
View SolutionIf the altitude from one vertex of a triangle bisects the opposite side; then the triangle is isosceles.
View SolutionDandE are points on equal sides ABandAC of an isosceles triangle ABC such that AD=AE . Prove that B,C,D,E are concylic.
View SolutionD and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD=AE. Prove that B, C, D, E are concyclic.
View SolutionABC is an isosceles triangle such that AB=ACandAD is the median to base BC . Then, ∠BAD=
(a) 55∘
(b) 70∘
(c) 35∘
(d) 110∘
View Solution