A door is hinged at one and is free to rotate about a vertical axis [Fig.] Does its weight cause any torque the axis ? Given reason for you answer.
![A door is hinged at one and is free to rotate about a vertical axis [Fig.] Does its weight cause any torque the axis ? Given reason for you answer.](https://d10lpgp6xz60nq.cloudfront.net/physics_images/PR_XI_V01_C05_S01_306_Q01.png)
Consider the diagram , where weight of the door acts along negative y-axis.
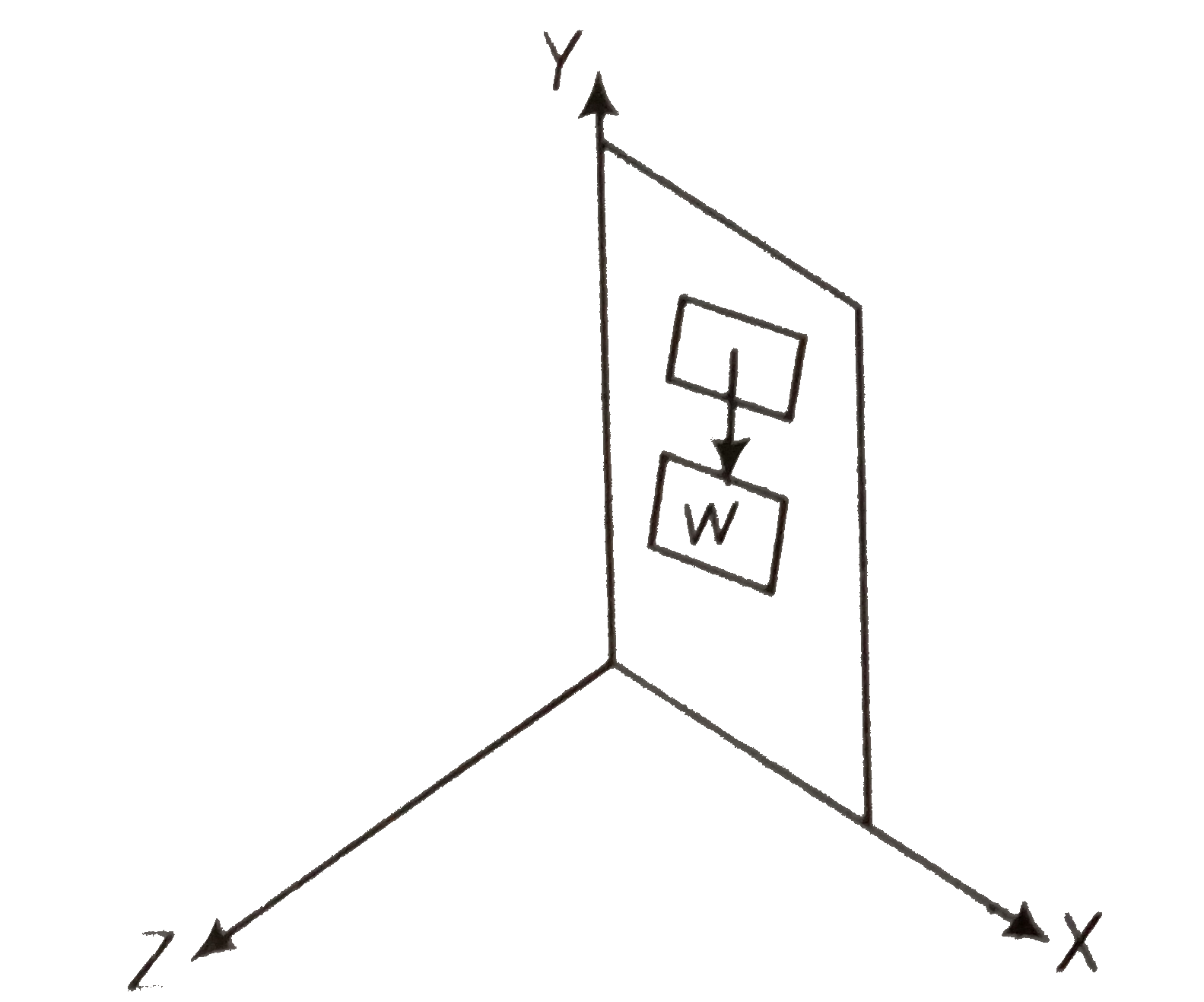
A force can produce torque only a direction normal to itself as τ=r×F so when the door is in the xy -plane the torque by gravity can only be along ± z direction never about an axis passing through y- direction .
Hence , the weight will not produce any torque about y-axis.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NCERT EXEMPLARChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:Long answer type questions
Explore 12 Videos
- OSCILLATIONSBook:NCERT EXEMPLARChapter:OSCILLATIONSExercise:MULTIPLE CHOICE QUESTIONS (MCQs)
Explore 40 Videos
- THERMAL PROPERTIES OF MATTERBook:NCERT EXEMPLARChapter:THERMAL PROPERTIES OF MATTERExercise:Very short Answer type Questions
Explore 15 Videos
Similar Questions
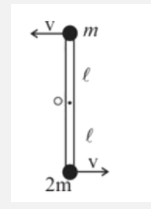
Two particles of masses m and 2m are attached to the massless rod of length 2l as shown in figure. The rod is hinged at its midpoint O and is free to rotate in vertical plane about hinge. The minimum speed v at the given instant so that it can complete the circle.
View SolutionA bullet of mass 10g and speed 500m/s is fired into a door and gets embedded exactly at the centre of the door. The door is 1.0m wide and weight 12kg. It is hinged at one end and rotates about a vertical axis practically without friction. Find the angular speed of the door just after the bullet embeds into it.(Hint. The moment of inertia of the door about the vertical axis at one end is ML2/3)
View Solution
Knowledge Check
When a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
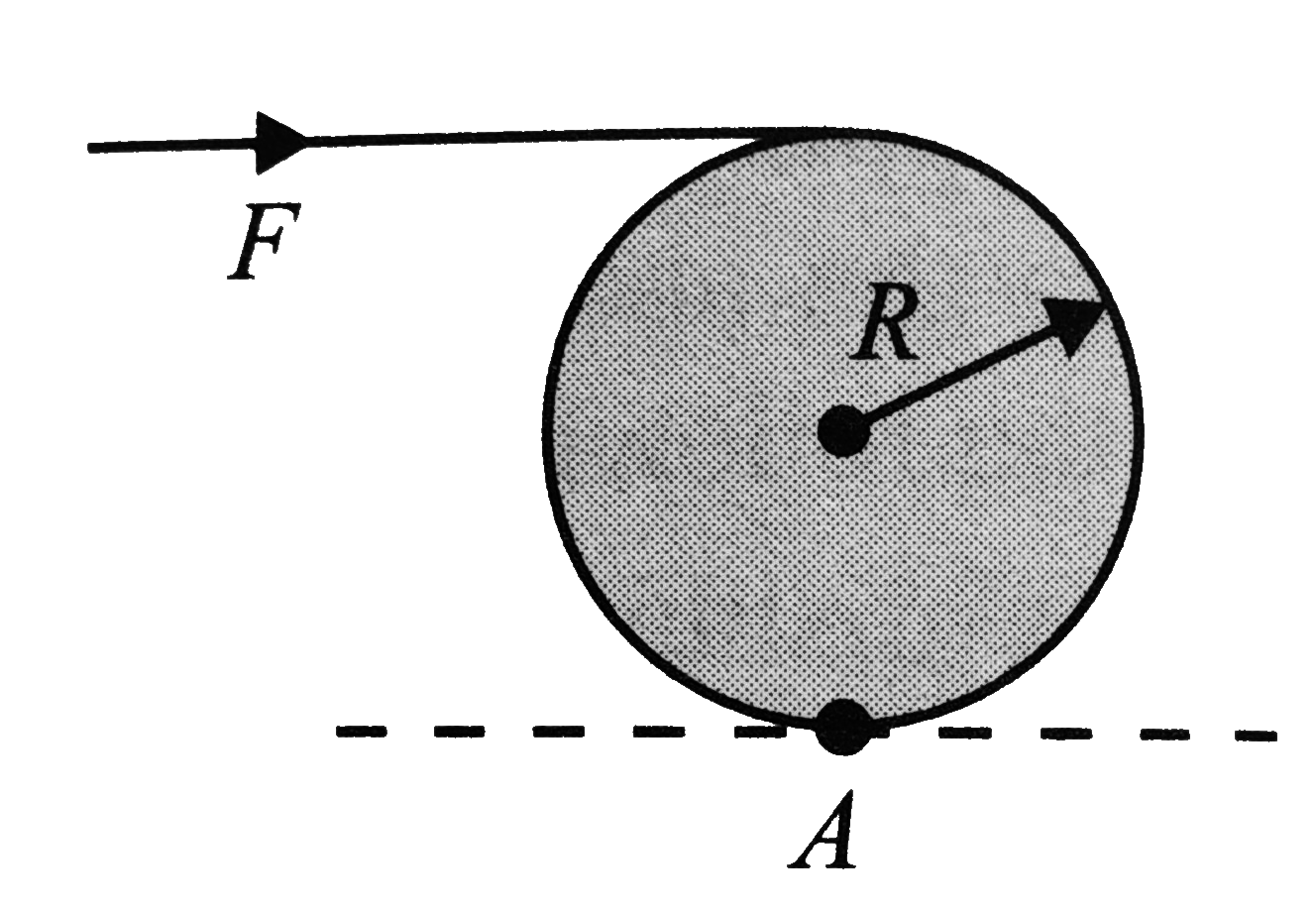
Component of reaction at the hinge in the vertical direction isA43mgBmgCMg2D23mgWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
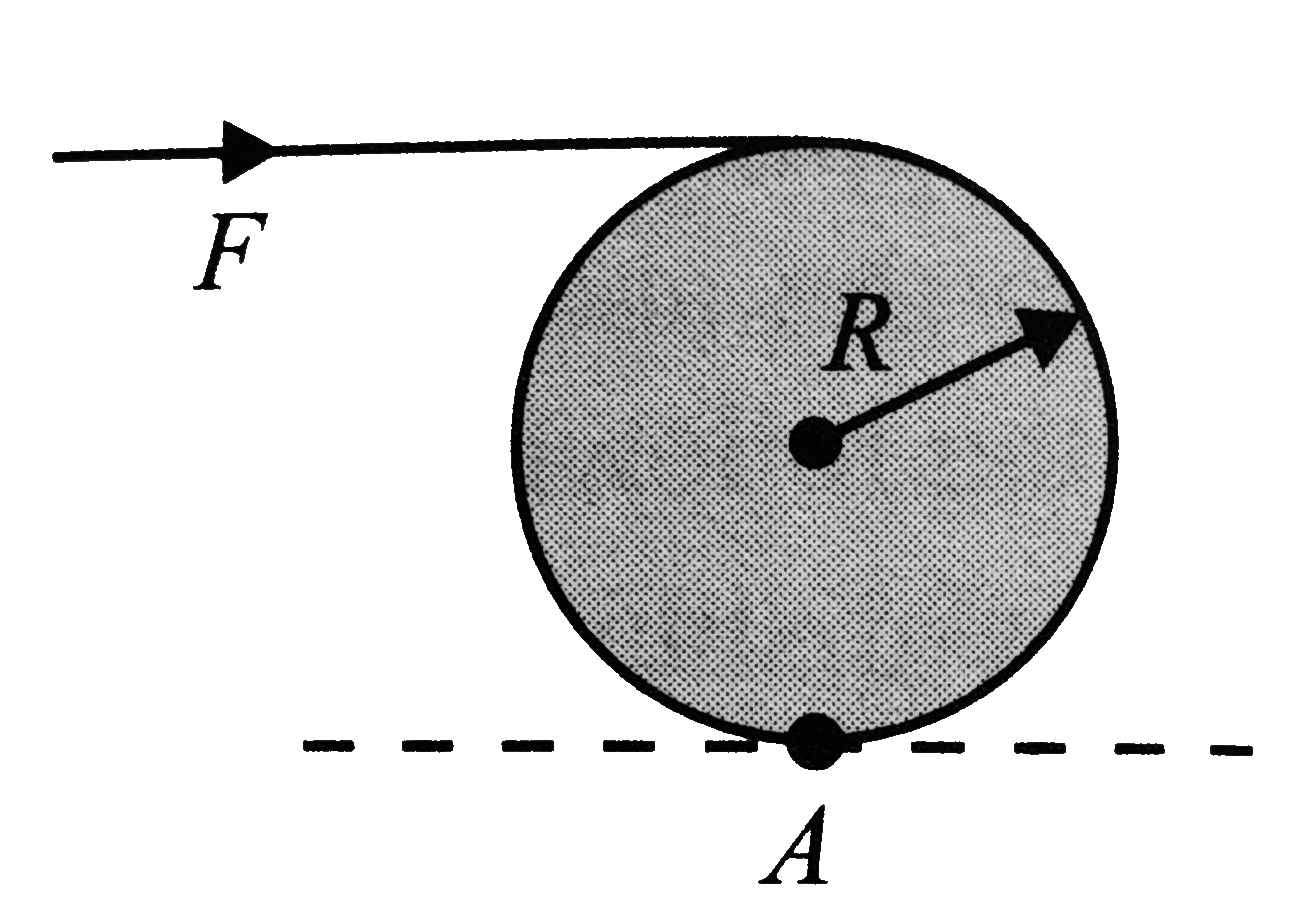
Component of reaction at the hinge in the horizontal direction isAF4BFCF3DF2The time taken by earth to complete one rotation about its axis is
A12 hoursB16 hoursC24 hoursD365 days
The figure shows three small spheres that rotate about a vertical axis. The perpendicular distance between the axis and the center of each sphere is given. Rank the three spheres according to their rotational inertia about that axis, greatest first.
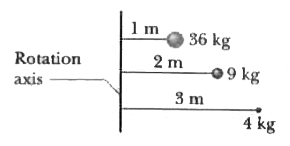
View SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
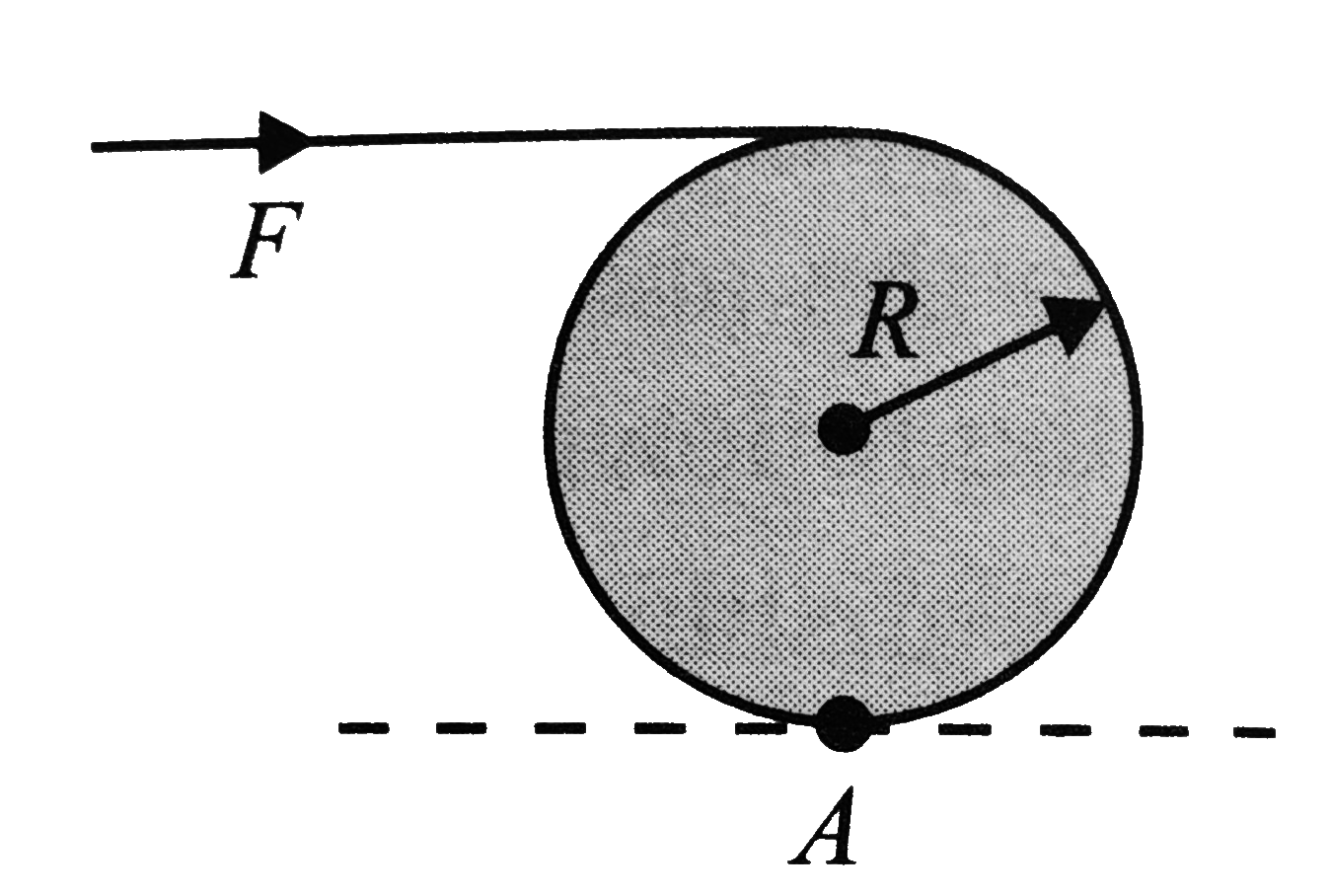
Tangential acceleration of the centre of mass is
View SolutionIf a horizontal cylindrical tube, partly filled with water is rapidly rotated about a vertical axis passing through its centre, the moment of inertia of the water about its axis will
View SolutionHow many degrees does the Earth rotate about its own axis in one hour?
View SolutionHow many degrees does the Earth rotate about its own axis in one hour?
View Solution

