(n−1) equal point masses each of mass m are placed at the vertices of a angular n-polygon. The vacant vertex has a position vector a with respect to the centre of the polygon. Find the position vector of centre of mass.
Let B be the position vector of the mass of a regular n- polygon , therefore for its centre of mass
fCM=(n−1)mb+ma(n−1)m+m=0(∵Centre of mass lies ata centre)
⇒(n−1)mb+ma=0
⇒b=−a(n−1)
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NCERT EXEMPLARCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - Long answer type questions
12 Videos
- OSCILLATIONSBOOK - NCERT EXEMPLARCHAPTER - OSCILLATIONSEXERCISE - MULTIPLE CHOICE QUESTIONS (MCQs)
40 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT EXEMPLARCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Very short Answer type Questions
15 Videos
Similar Questions
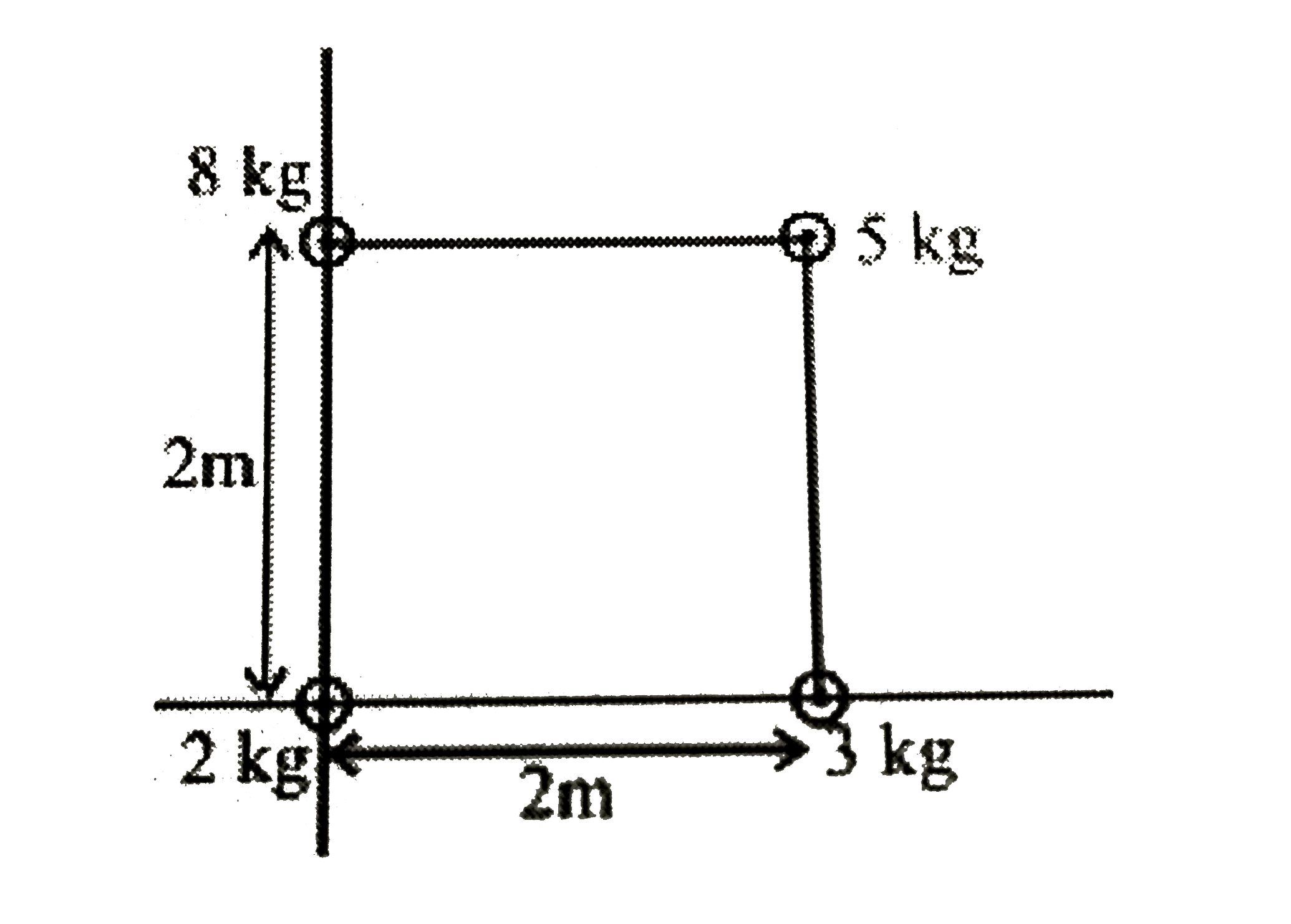
Position of the centre of mass is :-
View SolutionThree identical spheres , each of mass M , are placed at the corners of a right angled triangle with mutually perpendicular sides equal to 2 m . Taking their point of intersection as the origin , find the position vector of centre of mass
View Solution
Knowledge Check
Three identical spheres of mass M each are placed at the corners of an equilateral triangle of side 2 m. Taking one of the corners as the origin, the position vector of the centre of mass is
A√3(ˆi−ˆj)Bˆi√3+ˆjCˆi+ˆj/3Dˆi+ˆj/√3Three particles , each of mass m, are placed at the vertices of a right angled triangle as shown in figure. The position vector of the center of mass of the system is (O is the origin and ˆi,ˆj,ˆk are unit vectors)
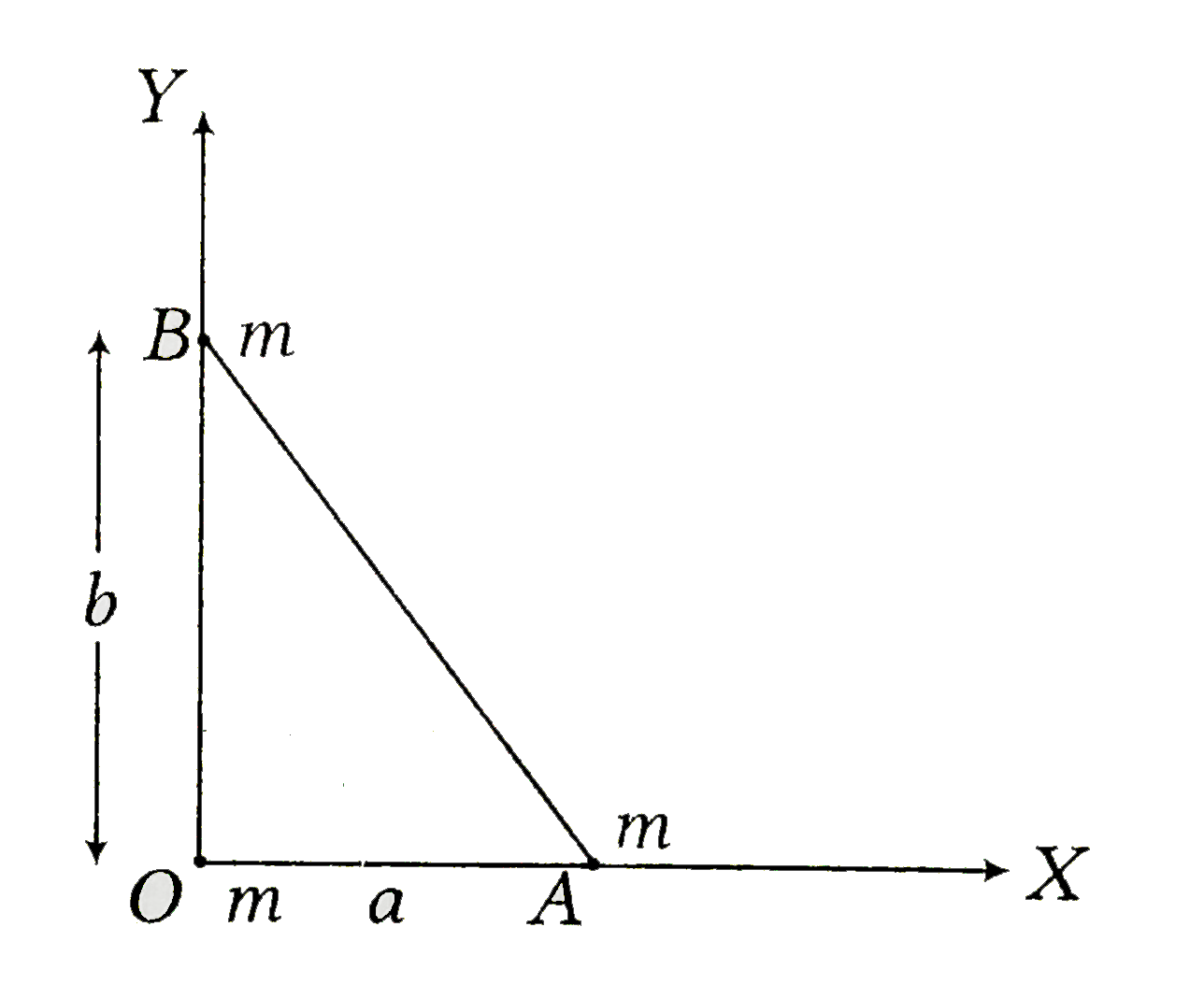 A13(aˆi−bˆj)B23(aˆi−bˆj)C23(aˆi+bˆj)D13(aˆi+bˆj)
A13(aˆi−bˆj)B23(aˆi−bˆj)C23(aˆi+bˆj)D13(aˆi+bˆj)Three identical spheres of mass m each are placed at the corners of an equilateral triangle of side 2m taking one of the corner as the origin the position vector of the centre of mass is
A√3(I∩−j∩)BI∩√3+j∩CI∩+j∩3DI∩+j∩√3
If a charge q is placed at each vertex of a regular polygon, the net electric field at its centre is zero. Show it.
View Solution(i) A regular polygon has 2016 sides and r is the radius of the circle circumscribing the polygon. Particles of equal mass are placed at 2015 vertices of the polygon. Find the distance of the centre of mass of the particle system from the centre of the polygon.
(ii) In the last problem you have been asked to remove any one particle from the system so that the centre of mass of the remaining 2014 particles lies farthest from the geometrical centre of the polygon. Which particle will you remove ?
View SolutionFind out the position of centre of mass of two particle system.
View SolutionThree identical spheres of mass m each are placed at the corners of an equilateral triangle of side 2m taking one of the corner as the origin the position vector of the centre of mass is
View SolutionThree equal masses each of 50 g, are placed at the corners of a right angled isoceles triangle whose two equal sides are 5 cm each. The position of the centre of mass of the system is
View Solution
