What is correct explanation of 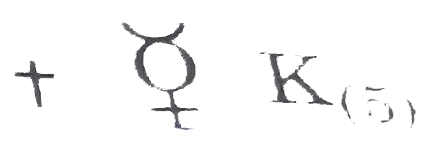
C−(1+2+(2))A(9+1)=G1
Zygomorphic, bisexual, sepals 5 and gamosepalous, petals five and papilionaceous, anthers the and monadelphous, ovary superior and monocarpellary
Zygomorphic, unisexual, sepals five and gemosepalous, petals five and polypetalous, anthers nine united and one-free, ovary superior and mono-carpellary
Zygomorphic, bisexual, sepals five and gamosepalous, petals five and popilionaceous, anthers ten and diadelphous, ovary superior and monocarpellary
Zygomorphic, bisexual, sepals five and united, petals five and united, anthers ten and diadelphous, ovary superior and monocarpellary
The correct Answer is:C
Step by step video, text & image solution for What is correct explanation of C-(1+2+(2))A_((9_+1)=G_(1) by Biology experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FAMILIES OF FLOWERING PLANTSBOOK - DINESH PUBLICATIONCHAPTER - FAMILIES OF FLOWERING PLANTSEXERCISE - CYG
10 Videos
- FAMILIES OF FLOWERING PLANTSBOOK - DINESH PUBLICATIONCHAPTER - FAMILIES OF FLOWERING PLANTSEXERCISE - BRAIN TEASERS -II
97 Videos
- FAMILIES OF FLOWERING PLANTSBOOK - DINESH PUBLICATIONCHAPTER - FAMILIES OF FLOWERING PLANTSEXERCISE - BRAIN TEASERS -II
97 Videos
- EXCRETORY PRODUCTS AND THEIR ELIMINATIONBOOK - DINESH PUBLICATIONCHAPTER - EXCRETORY PRODUCTS AND THEIR ELIMINATIONEXERCISE - Check your graps
10 Videos
- FLOWERBOOK - DINESH PUBLICATIONCHAPTER - FLOWEREXERCISE - MULTIPLE CHOICE
250 Videos
Similar Questions
The given floral formula is exemplified by [%ma≤K5C1+2+(2)A9+1G1]
View SolutionAssetion: a1,a2,a3,…………. an are not in G.P. Reason: an+1=an (A) Both A and R are true and R is the correct explanation of A (B) Both A and R are true R is not te correct explanation of A (C) A is true but R is false. (D) A is false but R is true.
View Solution
Knowledge Check
If a,a1,a2,a3,a2n,b are in A.P. and a,g1,g2,g3,,g2n,b . are in G.P. and h s the H.M. of aandb, then prove that a1+a2ng1g2n+a2+a2n−1g1g2n−1++an+an+1gngn+1=2nh
A2nHB2nHCnHDnHIf A1,A2 be two A.M.'s and G1,G2 be two G.M.,s between a and b, then A1+A2G1G2 is equal to
Aa+b2abB2aba+bCa+babDa+b√abIf A1,A2 be two A.M.'s and G1,G2 be two G.M.,s between a and b, then A1+A2G1G2 is equal to
Aa+b2abB2aba+bCa+babDa+b√ab
If A1 and A2 are two A.M.s between a and b and G1 and G2 are two G.M.s between the same numbers then what is the value of A1+A2G1G2
View SolutionShow that the equation of the straight line through (α,β) and through the point of intersection of the lines a1x+b1y+c1=0anda2x+b2y+c2=0 is a1x+b1y+c1a1α+b1β+c1=a2x+b2y+c2a2α+b2β+c2
View SolutionStatement 1 : 3,6, 12 are in GP, then 9, 12, 18 are in H. P.Statement 2: If three consecutive terms of a G.P. are positive and if middle term is added in these terms,then resultant will be in H.P(A)STATEMENT-1 is true, STATEMENT-2 is true and STATEMENT-2 is correct explanation forSTATEMENT-1STATEMENT-1 is true, STATEMENT-2 is true and STATEMENT-2 is not correct explanation forSTATEMENT-1STATEMENT-1 is true, STATEMENT-2 is falseSTATEMENT-1 is false, STATEMENT-2 is true(B)(C)(D)
View SolutionIf A1,A2 be two A.M. and G1,G2 be two G.M.s between aandb then A1+A2G1G2 is equal to a+b2ab b. 2aba+b c.a+bab d. a+b√ab
View Solutionf(x) and g(x) are polynomical of degree 2 such that ∣∣∣∫a2a1(f(x)−1)dx∣∣∣=∣∣∣∫b2b1(g(x)−1)dx∣∣∣
where a1,a2(a2>a1) are roots of equation f(x)=1 and b1,b2(b2>b1) are roots of equation g(x)=1. If f(x) and g(x) are positive constant and
∣∣∣∫a2a1f((x))dx∣∣∣=(a2−a1)−∣∣∣∫b2b1(f(x)−1)dx∣∣∣ but ∣∣∣∫b2b1(g(x))dx∣∣∣≠(b2−b1)−∣∣∣∫b2b1(g(x)−1)dx∣∣∣then
View Solution
