The given floral formula is exemplified by [%ma≤K5C1+2+(2)A9+1G1]
Aloe. Asparagus
Indigofera Tronum
Petunia, Datura
Groundnut , Turnip
Step by step video & image solution for The given floral formula is exemplified by [% male K_5C_{1+2+(2)} A_(9+1)G_1] by Biology experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
The given dental formula is exemplified by
31423143×2=42ALemurBKangarooCMan (adut)DDogWhat is correct explanation of
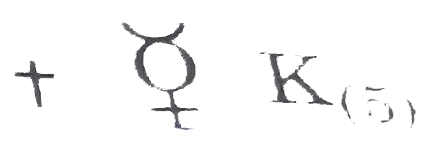
C−(1+2+(2))A(9+1)=G1AZygomorphic, bisexual, sepals 5 and gamosepalous, petals five and papilionaceous, anthers the and monadelphous, ovary superior and monocarpellaryBZygomorphic, unisexual, sepals five and gemosepalous, petals five and polypetalous, anthers nine united and one-free, ovary superior and mono-carpellaryCZygomorphic, bisexual, sepals five and gamosepalous, petals five and popilionaceous, anthers ten and diadelphous, ovary superior and monocarpellaryDZygomorphic, bisexual, sepals five and united, petals five and united, anthers ten and diadelphous, ovary superior and monocarpellaryTo which family following floral formula is related?
Floral Formula : ⊕O+−K3+3A3+3G−(3)AFabaceaeBSolanaceaeCLiliaceaeDCruciferae
If A1,A2,A3,…,An are n points in a plane whose coordinates are (x1,y1),(x2,y2),(x3,y3),…,(xn,yn) respectively. A1A2 is bisected in the point G1:G1A3 is divided at G2 in the ratio 1:2,G3A5 at G4 in the1 : 4 and so on untill all the points are exhausted. Show that the coordinates of the final point so obtained are x1+x2+.....+xnn and y1+y2+.....+ynn
View SolutionIf a,a1,a2,....,a10,b are in A.P. and a,g1,g2,....,g10,b are in G.P. and h is the H.M. betweein a and b, then a1+a2+...+a10g1g10+a2+a3+....+a9g2g9+......+a5+a6g5g6 is
View SolutionIf a,a1,a2,a3,a2n,b are in A.P. and a,g1,g2,g3,,g2n,b . are in G.P. and h s the H.M. of aandb, then prove that a1+a2ng1g2n+a2+a2n−1g1g2n−1++an+an+1gngn+1=2nh
View SolutionGiven for the following equilibrium taking place in 1 L flask at 300 K. PC15(g)⇔PC13(g)+C12(g) , Kc=4 Thus, degree of dissociations of PC15 (g) is
View SolutionIf A1,A2 be two A.M.'s and G1,G2 be two G.M.,s between a and b, then A1+A2G1G2 is equal to
View Solution

