Two infinitely long straight wires lie in the xy-plane along the lines . The wire located at carries a constant current and the wire located at carries a constant current . A circular loop of radius R is suspended with its centre at and in a plane parallel to the xy-plane. This loop carries a constant current ? in the clockwise direction as seen from above the loop. The current in the wire is taken to be positive if it is in the direction. Which of the following statements regarding the magnetic field is (are) true?
If , then cannot be equal to zero at the origin (0, 0, 0)
If and , then can be equal to zero at the origin (0, 0, 0)
If and then can be equal to zero at the origin (0, 0, 0)
If , then the z-component of the magnetic field at the centre of the loop is
The correct Answer is:A, B, D
B due to at origin , B due to at origin
B due to I at origin
So if A is correct
So if I will have a value for which B can be zero B is correct
so if has to be alogn C is incorrect
If B at the centre of loop D is correct.
A Z- component of B due to & cancel out.

Similar Questions
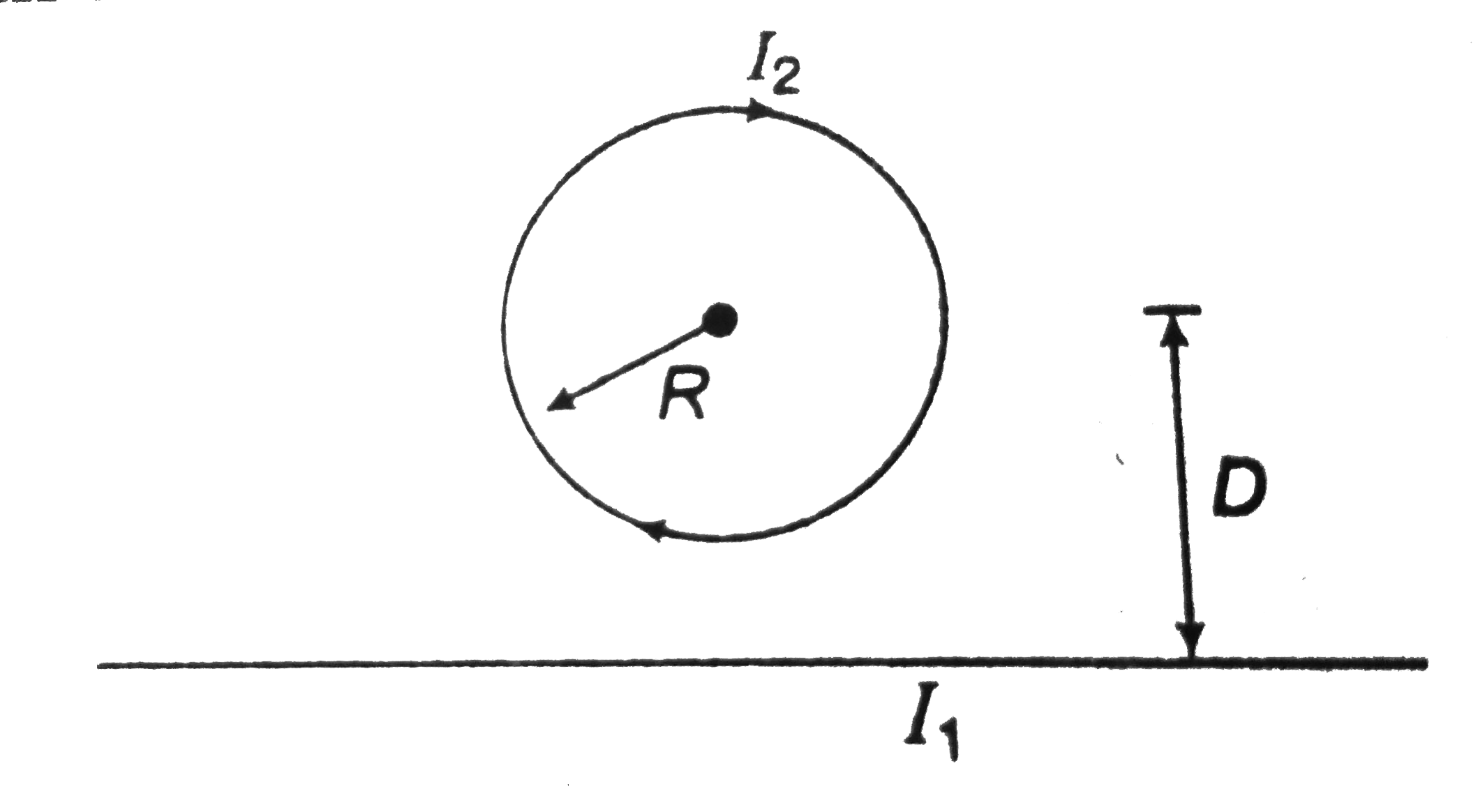
A circular loop of radius R carries current I2 in a clockwise direction as shown in figure. The centre of the loop is a distance D above a long, straight wire. What are the magnitude and direction of the current I1 in the wire if the magnetic field at the centre of loop is zero?
View SolutionA circular loop of wire of radius R is bent about its diameter along two mutually perpendicular planes as shown in Fig. If the loop carries a current I, then determine its magnetic moment.
View Solution
Knowledge Check
A circular loop of radius R, carrying I lies in xy-plane with its centre at origin. The total magnetic flux through xy-plane is :
Adirectly proportional to RBdirectly proportional to ICinversely proportional to RDzeroA circular loop of radius R, carrying I lies in xy-plane with its centre at origin. The total magnetic flux through xy-plane is :
Adirectly proportional to RBdirectly proportional to ICinversely proportional to RDzeroA circular loop of radius R , carrying I, lies in x−y plane with its origin . The total magnetic flux through x−y plane is
Adirectly proportional to IBdirectly proportional to RCinversly proportional to RDzero
Two concentric circular loops one of radius R and other of radius 2R lie in the xy plane with the origin as their common center . Smaller loop carries current I1 in anticlockwise direction and larger loop carries I2 in clockwise direction with I2>2I1,vec(B)(x,y) denotes magnetic feld at a point (x,y) in xy-plane. Which of the following statements are correct?
View SolutionConsider a long infinite wire carrying a time varying current i=kt(k>0). A circular loop of radius a and resistance R is placed with its centre at a distance d from the wire (a<<d). Find out the induced current in the loop?
View SolutionA circular loop has radius R and carries current I2 in a clockwise direction (as shown in Fig.) The centre of the loop is at a distance D above a long, straight wire. What are the magnitude and direction of the current I1 in the wire if the magnetic field at the center of the loop is zero?

View SolutionA current − carrying circular loop of radius R is placed in the XY− plane with centre at the origin. Half of the loop with x>0 is now bent so that is now lies in the XY− plane
View SolutionTwo infinitely long, thin, insulated, straight wires lie in the x-y plane along the x- and y- axis respectively. Each wire carries a current I, respectively in the positive x-direction and positive y-direction. The magnetic field will be zero at all points on the straight line:
View Solution