An infinitely long hollow coducting cylinder with inner radius R2 and outer radus R carries a uniform current density along its length. The magnitude of the magnetic field |B| as a function of the radial distance r from the axis is best represented by




The correct Answer is:D
r= distance of a point from centre
For r≤R/2 using Ampere's circuital law, ∮B.dl or B1=μ0(Iin)
or B(2πr)=μ0(Iin) or B=μ02πIinr…….i
Since Iin=0⇒∴B=0 for R2≤r≤RIin=[πr2−π(R2)2]σs
Here σ= current per unit area. Substituting in eq. (i) we have

B=m02π[πr2−πR24]σr=μ0σ2r(r2−R24) at r=R2,B=0 at r=R,B=3μ0σR8 For r≥R
Iin=ITotal=I (say) Therefore, substituting in eq. (i) we have B=μ02π.Ir or B∝1r
Similar Questions
A long, straight wire of radius R carries a current distributed uniformly over its cross section. The magnitude of the magnetic field is
View SolutionA thin but long, hollow, cylindrical tube of radius r carries a current i along its length. Find the magnitude of the magnetic field at a distance r/2 from the surface (a) inside the tube (b) outside the tube.
View Solution
Knowledge Check
An infinitely long hollow conducting cylinder with inner radius R2 and outer radius R carries a uniform current ra density along its length . The magnitude of the magnetic field , ∣∣→B∣∣ as a function of the radial distance r from the axis is best represented by
A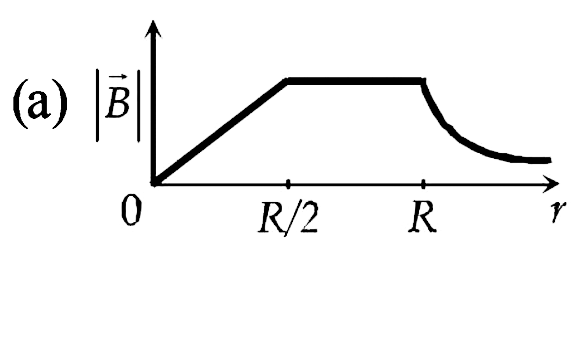 B
B C
C D
D
Figure shows the cross-sectional view of the hollow cylindrical conductor with inner radius 'R' and outer radius '2R', cylinder carrying uniformly distributed current along it's axis. The magnetic induction at point 'P' at a distance 3R2 from the axis of the cylinder will be
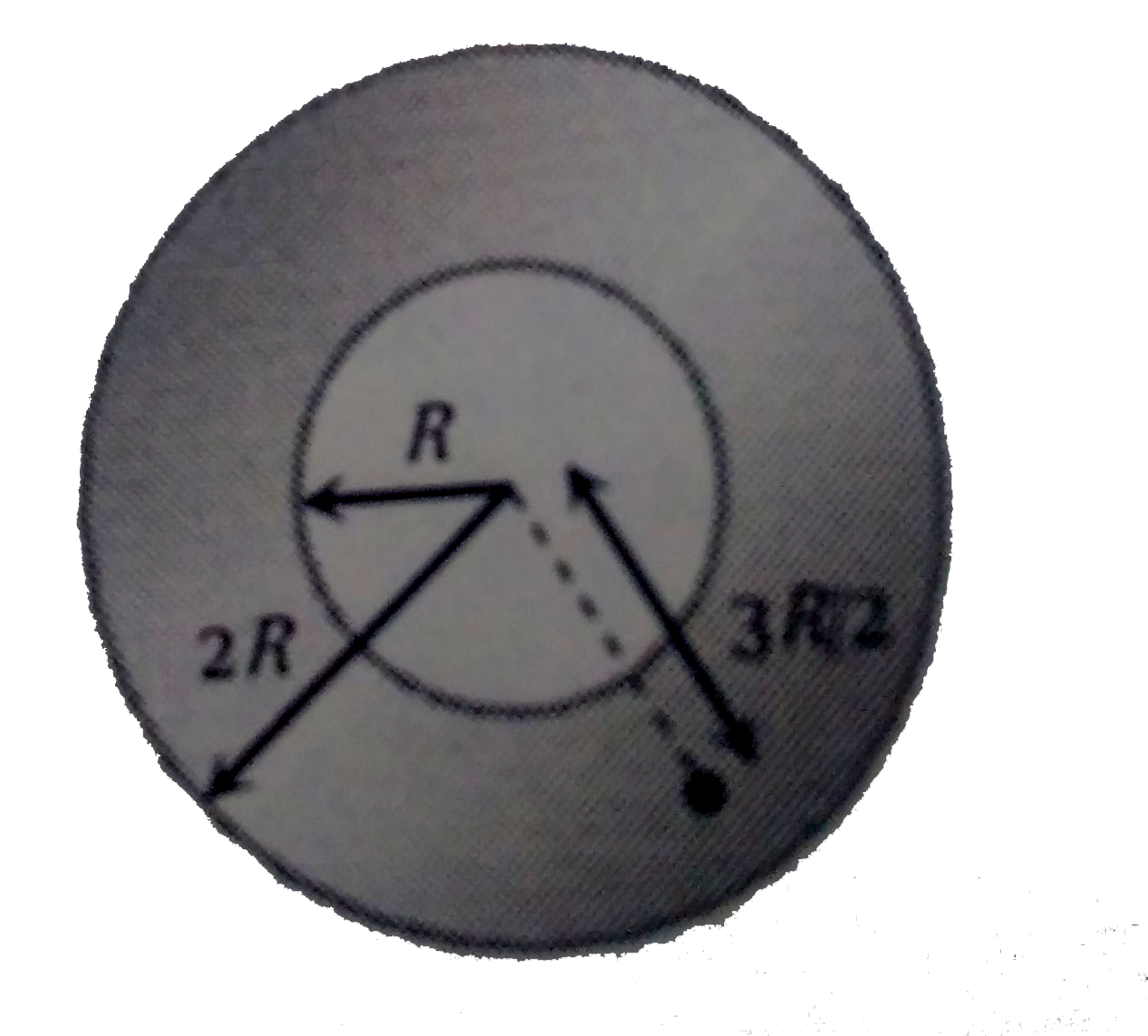 AZeroB5μ0i72πRC7μ0i18πRD5μ0i36πR
AZeroB5μ0i72πRC7μ0i18πRD5μ0i36πRA cylindrical conductor of radius R is carrying constant current. The plot of the magnitude of the magnetic field, B with the distance, d from the centre of the conductor , is correctly represented by the figure:
A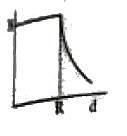 B
B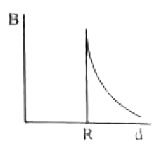 C
C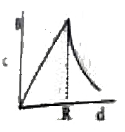 D
D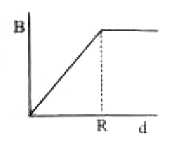
A thick current carrying cable of radius 'R' carries current 'I' uniformly distributed across its crosssection. The variation of magnetic field B(r) due to cable with distance 'r' from the axis of the cable is represented by.
View Solution.Figure shows the cross-sectional view of the hollow cylindrical conductor with inner radius R and outer radius '2R',cylinder is carrying uniformly distributed current along it's axis.The magnetic induction at point p at a distance 3R2 from the axis of the cylinder will be 5μ0in×9πR .Find n?
View SolutionA cylindrical conductor of radius R is carrying a constant current. The plot of the magnitude of the magnetic field, B with the distance, d from the centre of the conductor, is correctly represented by the figure
View SolutionThe figure shows the cross-section of a long conducting cylinder of inner radius a and outer radius b. The cylinder carries a current whose current density J=Cr2 where C is a constant. What is the magnitude of the magnetic field B at a point r, where a<r<b?
View SolutionA cylinderical conductor of radius R is carrying constant current. The plot of the magnitude of the magnetic field, B with the distance, d from the centre of the conductor , is correctly represented by the figure:
View Solution