Two very long straight parallel wires, parallel to y-axis, carry currents 41 and I, along+y direction and-y direaction respectively. The wires are passes through the x-axis at the points $(d, 0, 0)$ and $(- d, 0, 0)$ respectively. The graph of magnetic field z-component as one moves along the x-axis from $x = - d$ to $x = + d$ , is best given by

ocr_image

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

Two long parallel wires, AB and CD, carry equal currents in opposite directions. They lie in the x-y plane, parallel to the x-axis, and pass through the points (0,-a,0) and (0,a,0) respectively, Figure. The resultant magnetic field is:

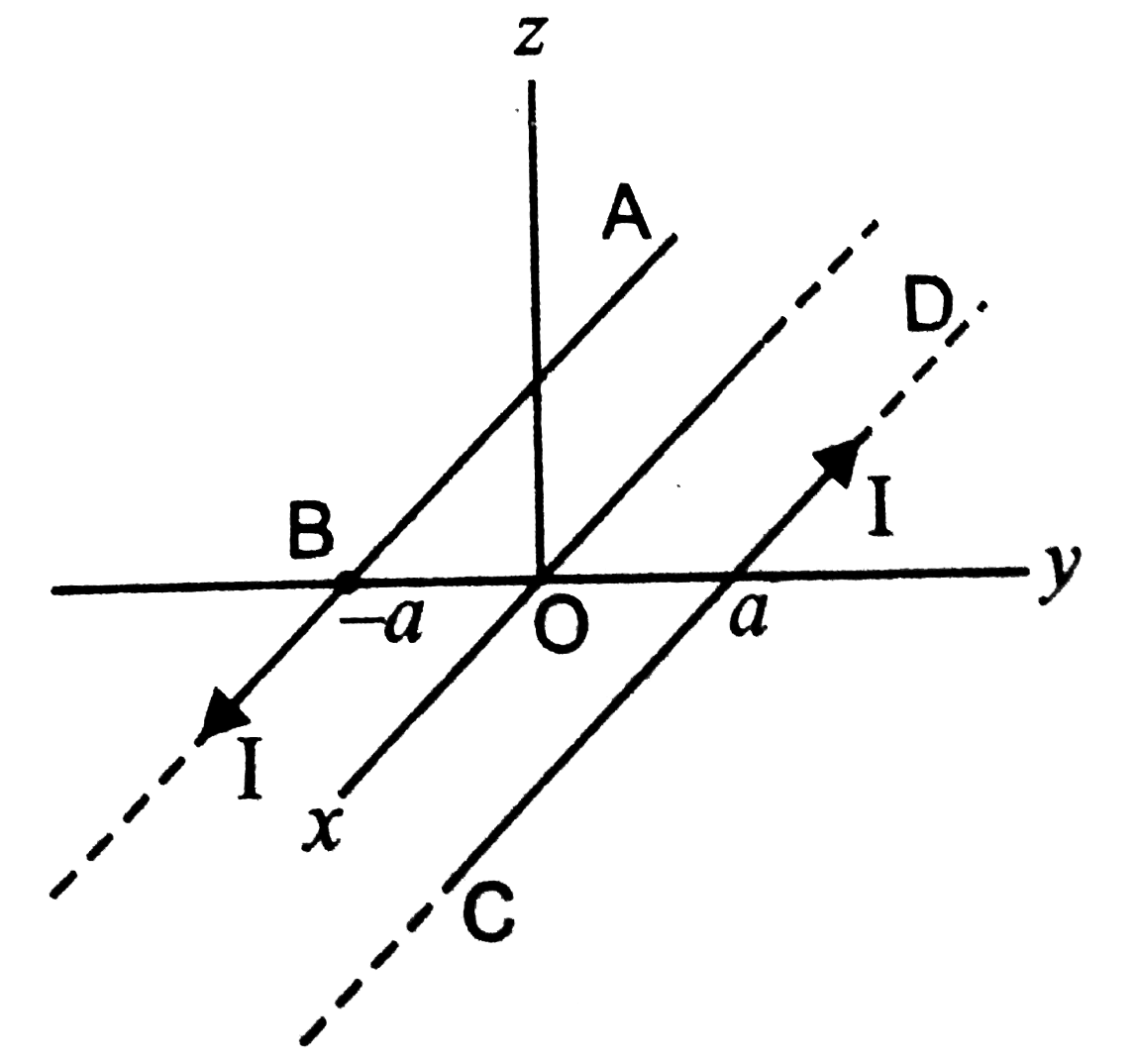Azero on the x-axis
Bmaximum on the x-axis
Cdirected along the z-axis at the origin, but not at other points on the z-axis
Ddirected along the z-axis at all points on the z-axis.
A long straight wire along the z-axis carries a current I in the negative z-direction. The magnetic vector field $\to B$ at a point having coordinnates (x, y) in the z = 0 plane is
A $\frac{μ_{0} I (y ˆ i - x ˆ j)}{2 π (x^{2} + y^{2})}$
B $\frac{μ_{0} I (x ˆ i + y ˆ j)}{2 π (x^{2} + y^{2})}$
C $\frac{μ_{0} I (x ˆ j - y ˆ i)}{2 π (x^{2} + y^{2})}$
D $\frac{μ_{0} I (x ˆ i - y ˆ j)}{2 π (x^{2} + y^{2})}$
A long straight wire along the $z - a ξ s$ carries a current $I$ in the negative $z - d i r e c t i o n$ . The magnetic vector field $\to B$ at a point having coordinates (x,y) in the $Z = 0$ plane is
A $\frac{μ_{0} I (y ˆ i) - x ˆ j}{2 π (x^{2} + y^{2})}$
B $\frac{μ_{0} I (x ˆ i) + y ˆ j}{2 π (x^{2} + y^{2})}$
C $\frac{μ_{0} I (x ˆ j) - y ˆ i}{2 π (x^{2} + y^{2})}$
D $\frac{μ_{0} I (y x ˆ i) - y ˆ j}{2 π (x^{2} + y^{2})}$