A thin sheet of width 2a is placed in the x-y plane between the lines x=−a and x=a. The sheet is very long in the -y and +y directions. It carries a current l towards the +y direction. This current is uniformly distributed over the width of the sheet. The magnitude of magnetic fiedl at the point P(2a,0) due to the sheet is (1n)(μ0Iπa)loge3. Here the value of n is ______________.
The correct Answer is:4
To solve the problem, we need to calculate the magnetic field at point P(2a, 0) due to a thin sheet of width 2a carrying a uniformly distributed current I in the +y direction. Here’s a step-by-step breakdown of the solution:
Step 1: Understanding the Setup
We have a thin sheet of width 2a placed in the x-y plane between the lines x = -a and x = a. The current I flows in the +y direction, uniformly distributed across the width of the sheet.
Step 2: Define the Current Density
The current density (λ) can be defined as the current per unit length across the width of the sheet:
λ=I2a
Step 3: Consider an Element of Current
Consider a differential element of current (di) at a position x within the sheet. The width of this element is dx, and the current through this element is given by:
di=λdx=I2adx
Step 4: Calculate the Magnetic Field Contribution (dB)
The magnetic field contribution (dB) at point P due to the current element di can be calculated using the formula for the magnetic field around a long straight wire:
dB=μ0di2πr
where r is the distance from the current element to point P. Since point P is at (2a, 0), the distance r from the current element at position x is:
r=2a−x
Thus, we have:
dB=μ02π(2a−x)⋅I2adx
Step 5: Integrate to Find the Total Magnetic Field (B)
To find the total magnetic field at point P, we need to integrate dB from x = -a to x = a:
B=∫a−adB=∫a−aμ0I4πa(2a−x)dx
Step 6: Change of Variables
Let u=2a−x, then du=−dx. The limits change accordingly:
- When x=−a, u=3a
- When x=a, u=a
Thus, the integral becomes:
B=μ0I4πa∫a3a−duu=μ0I4πa(lnu)a3a
This simplifies to:
B=μ0I4πa(lna−ln3a)=μ0I4πalna3a=μ0I4πaln13=−μ0I4πaln3
Step 7: Final Expression for B
The magnitude of the magnetic field at point P is:
B=μ0I4πaln3
Step 8: Relate to Given Expression
The problem states that the magnetic field can be expressed as:
B=1n⋅μ0Iπaln3
By comparing the two expressions for B, we find:
μ0I4πaln3=1n⋅μ0Iπaln3
Cancelling common terms, we get:
14=1n
Thus, n=4.
Conclusion
The value of n is:
4
We have a thin sheet of width 2a placed in the x-y plane between the lines x = -a and x = a. The current I flows in the +y direction, uniformly distributed across the width of the sheet.
The current density (λ) can be defined as the current per unit length across the width of the sheet:
λ=I2a
Consider a differential element of current (di) at a position x within the sheet. The width of this element is dx, and the current through this element is given by:
di=λdx=I2adx
The magnetic field contribution (dB) at point P due to the current element di can be calculated using the formula for the magnetic field around a long straight wire:
dB=μ0di2πr
where r is the distance from the current element to point P. Since point P is at (2a, 0), the distance r from the current element at position x is:
r=2a−x
Thus, we have:
dB=μ02π(2a−x)⋅I2adx
To find the total magnetic field at point P, we need to integrate dB from x = -a to x = a:
B=∫a−adB=∫a−aμ0I4πa(2a−x)dx
Let u=2a−x, then du=−dx. The limits change accordingly:
- When x=−a, u=3a
- When x=a, u=a
B=μ0I4πa∫a3a−duu=μ0I4πa(lnu)a3a
This simplifies to:
B=μ0I4πa(lna−ln3a)=μ0I4πalna3a=μ0I4πaln13=−μ0I4πaln3
The magnitude of the magnetic field at point P is:
B=μ0I4πaln3
The problem states that the magnetic field can be expressed as:
B=1n⋅μ0Iπaln3
By comparing the two expressions for B, we find:
μ0I4πaln3=1n⋅μ0Iπaln3
Cancelling common terms, we get:
14=1n
Thus, n=4.
The value of n is:
4
Similar Questions
In Fig. a larger metal sheet of width w carries a current I(uniformly distributed in its width w). Find the magnetic field at point P which lies on the plane of the sheet.


View SolutionTwo large metal sheets carry surface currents as shown in figure . The current through a strip of width dl is Kdl where K is a constant . Find the magnetic field at the points P,Q and R.

View Solution
Knowledge Check
A wire loop carrying current I is placed in the x-y plane as shown. Magnetic induction at P is
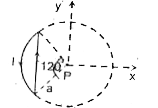 Aμ0I2a(√3π−13)Bμ0I2a(13−π√3)Cμ0I2a(13+√3π)Dμ0I2a(√3π−13)
Aμ0I2a(√3π−13)Bμ0I2a(13−π√3)Cμ0I2a(13+√3π)Dμ0I2a(√3π−13)A long straight wire along the z−aξs carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
Aμ0I(yˆi)−xˆj2π(x2+y2)Bμ0I(xˆi)+yˆj2π(x2+y2)Cμ0I(xˆj)−yˆi2π(x2+y2)Dμ0I(yxˆi)−yˆj2π(x2+y2)Axis of a solid cylinder of infinite length and radius R lies along y-axis. It carries a uniformly distributed current I along +y direction. Magnetic field at a point (R/2,y,R/2) is
Aμ0I4πR(ˆi−ˆk)Bμ0I2πR(ˆj−ˆk)Cμ0I4πRˆjDμ0I4πR(ˆi+ˆk)
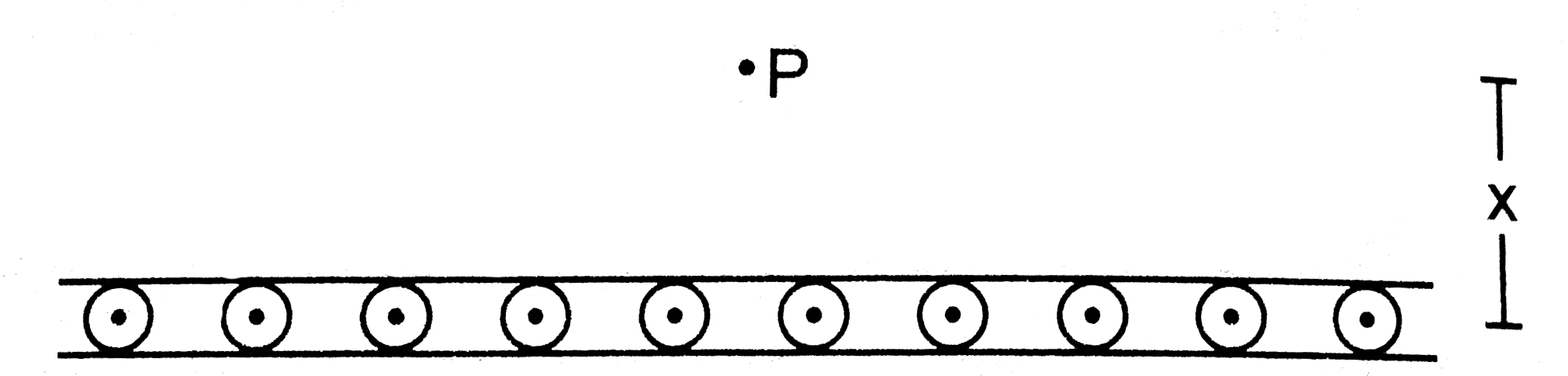
Figure shows a cross section of a large metal. Sheet carrying an electric current along its surface. The current in a strip of width dl is Kdl where K is a constant. Find the magnetic field at a point P at a distance x from the metal sheet.
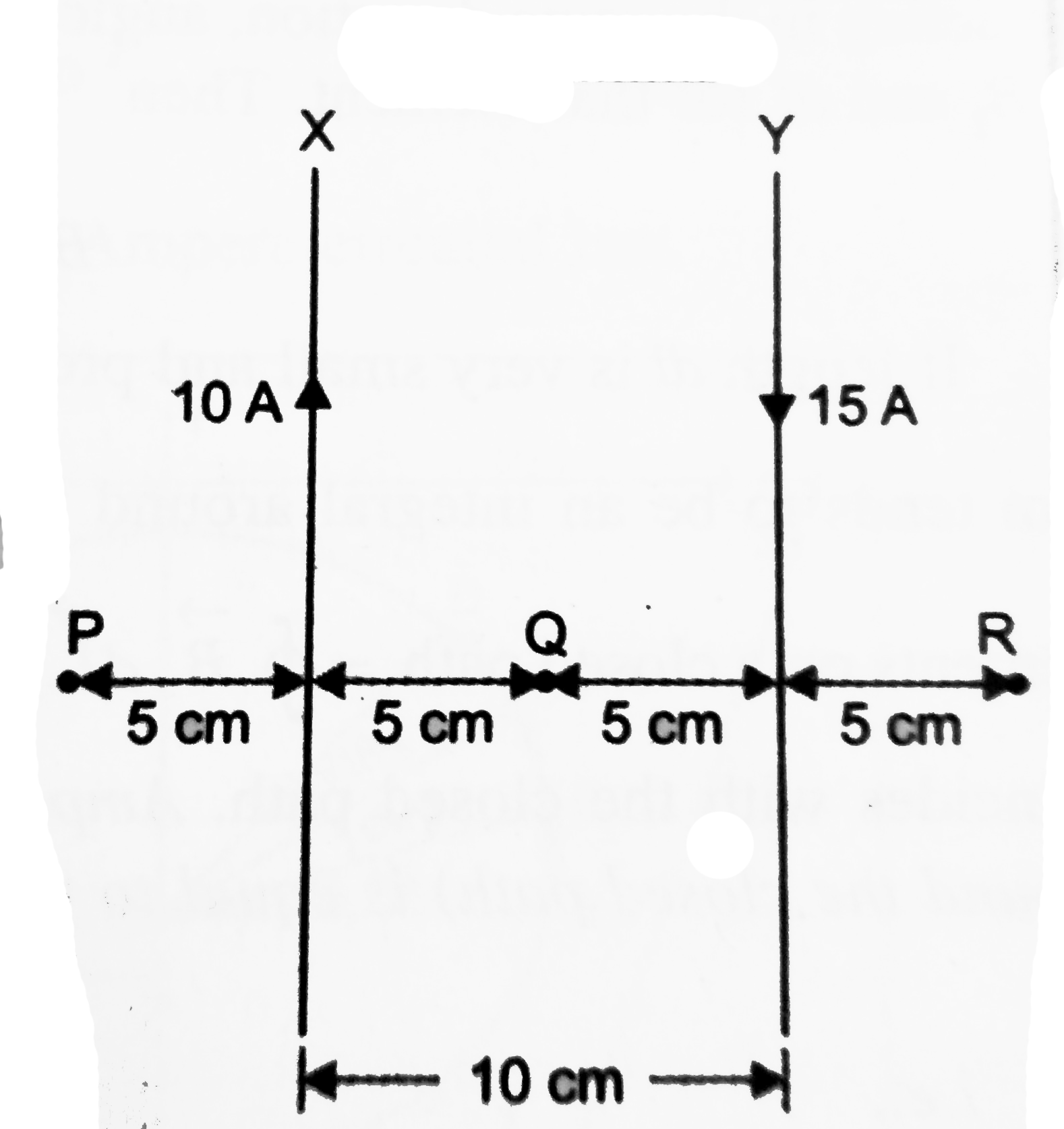
View SolutionThere are two parallel current carrying wires X and Y as shown in figure. Find the magnitude and direction of the magnetic field at points, P, Q and R.
View SolutionA long wire is along x=0,z=d and carries current in positive y direction. Another wire is along x=y,z=0 and carries current in direction making acute angle with positive x direction. Both the wires have current I. Find the magnitude of magnetic induction at (0,0,2d).
View SolutionA wire lying along y-axis from y=0 to y=1m carries a current of 2mA in the negative y-direction. The wire lies in a non uniform magnetic field given by B=(0.3Tm)yˆi+(0.4Tm)yˆj. The magnetic force on the entire wire is
View SolutionA long straight wire along the z-axis carries a current I in the negative z-direction. The magnetic vector field →B at a point having coordinnates (x, y) in the z = 0 plane is
View Solution