A capacitor C1 is charged to a potential V and connected as shown with capacitors C2andC3 both of which are initially uncharged. Capacitance of all capacitors is C. The ammeter is ideal. At t=01 switch S is closed. Pick the correct choice(s):
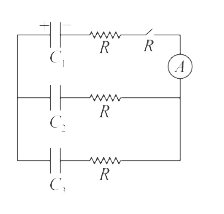
Just after t = 0, the ammeter reads 2V3R
Just after t = 0, rate of total heat dissipation in all resistors is 2V23R
After a long time, potential difference across C1isV3
If switch is kept closed for a long time, Total heat dissipation in all resistors is 16CV2
The correct Answer is:A, B, C
Due to the symmetrical situation of C2andC3, current
into them is always equal.
At t=0, C2andC3 are uncharged
So, applying KVL,
V−iR−2iR=0⇒ At t=0,i=V3R
⇒ Current out of C1=2i=2V3R, Rate of heat dissipation =i2R+i2R+(2i)2R=6i2R=2V23R
At steady state, each capacitor curries charge CV3 with all left plates carrying positive charge.
⇒Toal heat dissipation=Ui−Uf=12CV2−3(12C(V3)2)=13CV2.

Similar Questions
A capacitor of capacity C charged to potential "V" and " then connected to an identical uncharged capacitor then loss of energy is
View SolutionA capacitor of capacity C0 is charged to certain potential and enrgy stored in it is U0. Now this capacitor is connected in parrallel to uncharged capacitor of capacitance. C. Find the loss of energy.
View Solution
Knowledge Check
A capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
AC1VC1+C2BC2VC1+C2C1+C2C1D1−C2C1A capacity of capacity C1 is charged up to V volt and then connected to an uncharged capacitor of capacity C2. Then final potential difference across each will be
AC2VC1+C2B(1+C2C2)VCC1VC1+C2D(1−C2C1)VA capacitor of capacitance C1 is charged to a potential difference V and then connected with an uncharged capacitor of capacitance C2 a resistance R. The switch is closed at t = 0. Choose the correct option(s):
AThe initial current through the resistance is VRBThe current through the resistance as a function of time is i(t)=VRe−tτ where τ=R(C1C2C1+C2)CThe charge on capacitor C1 as a function of time is q1(t)=(C1VC1+C2)(C1+C2e−tτ)DAfter a long time, the potential difference across the capacitor C1is(C1C1+C2)V
Initially the capacitor is uncharged find the charge on capacitor as a function of time, if switch is closed at t=0.

View SolutionA capacitor C1 is charged to a p.d.V. The charging battery is then removed and the capacitor is connected to an uncharged capacitor C2. The final p.d. across the combination is
View SolutionA capacitor of capacitance C0 is charged to a potential V0 and is connected with another capacitor of capacitance C as Shown . After closing the switch S, the common potential across the two capacitors becomes V . The capacitance C is given by

View SolutionA capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
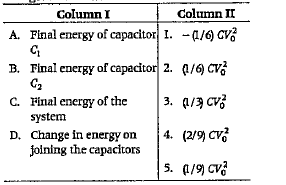
View SolutionA capacitor C1 of capacitance C is charged to a potential difference V0. The terminal of the charged capacitor are then connected to an uncharged capacitor C2of capacitance C/2. Match the entries of Column I with the entries of Column II and choose the correct option from the codes given below.
View Solution
