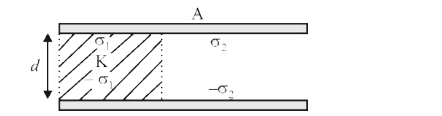
A parallel plate capacitor of area A and separation d is charged to potential difference V and removed from the charging source. A dielectric slab of constant thickness d and area $\frac{A}{2}$ is inserted, as shown in the figure. Let $σ_{1}$ be free charge density at the conductor-dielectric surface and $σ_{2}$ be the charge density at the conductor-vacuum surface. The incorrect statement is

The electric fields have different values inside the dielectric and in the free space between the plates

The ratio $\frac{σ_{1}}{σ_{2}}$ is equal to $\frac{2}{1}$

The new capacitance is $\frac{3 ε_{0} A}{2 d}$

The new potential difference is $\frac{2 V}{3}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

A parallel plate capacitor of area A and separation d is charged to potential difference V and removed from the changing source. A dielectric slab of constant K =2, thickness d and are area $\frac{A}{2}$ is inserted, as shown in the figure. Let $σ_{1}$ be free charge density at the conductor-dielectric surface and $σ_{2}$ be the charge density at the conductor-vacuum surface

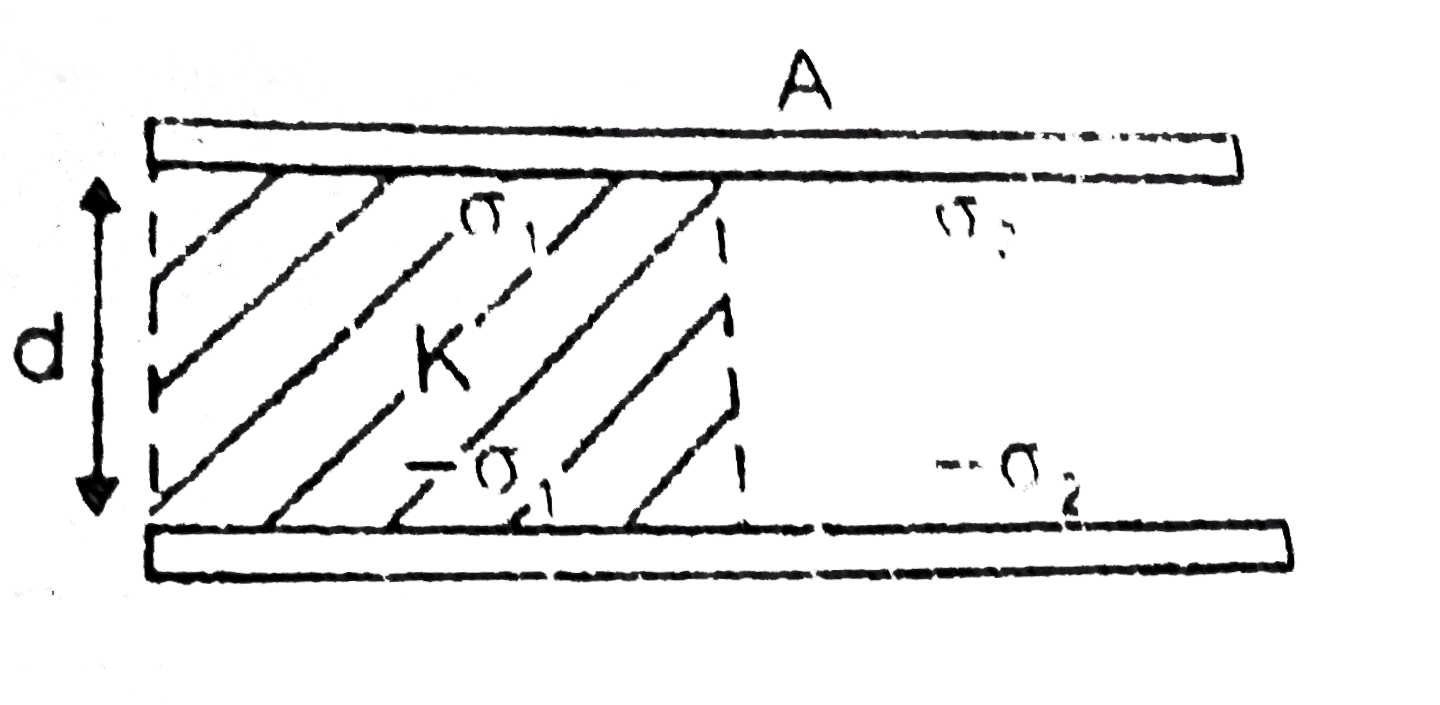AThe electric field have same value inside the dielectric as in the free space between the plates
BThe ratio $\frac{σ_{1}}{σ_{2}}$ is equal to $\frac{2}{1}$
CThe new capcitance is $\frac{3 \in_{0} A}{2 d}$
DThe new potential difference is $\frac{2}{3} V$
A parallel plate capacitor is charged to a potential difference of 100V and disconnected from the source of emf. A slab of dielectric is then inserted between the plates. Which of the following three quantities change?
Aonly (i) and (ii)
Bonly (i) and (iii)
Conly (ii) and (iii)
DAll (i),(ii) and (iii)
A parallel plate capacitor has plates with area A and separation d. A battery charges the plates to a potential difference $V_{0}$ . The battery is then disconnected and a dielectric slab of thikness d is introduced. The ratio of the enrgy stored in the capacitor before and after the slab is introduced, is
AK
B $\frac{1}{K}$
C $\frac{A}{d^{2} K}$
D $\frac{d^{2} K}{A}$