A solid body X of heat capacity C is kept in an atmosphere whose temperature is TA=300K. At time t=0 the temperature of X is T0=400K. It cools according to Newton's law of cooling. At time t1, its temperature is found to be 350K. At this time (t1), the body X is connected to a large box Y at atmospheric temperature is T4, through a conducting rod of length L, cross-sectional area A and thermal conductivity K. The heat capacity Y is so large that any variation in its temperature may be neglected. The cross-sectional area A of hte connecting rod is small compared to the surface area of X. Find the temperature of X at time t=3t1.
The correct Answer is:(300+12.5e(−2KAt1)CL)
(300+12.5−2KAt1CLe)
In the first part of the question (t≤t1)
TA=300KX
At t=0,TX=T0=400Kandatt=t1,TX=T1=350K
Temperature of atmosphere, TA=300K (constant)
This cools down according to Newton’s law of cooling.
Therefore, rate of cooling ∝ temperature difference.
∴(−dTdt)=k(T−TA)⇒dTT−TA=kdt⇒∫T1T0dTT−TA=−k∫t10dt
⇒ln(T1−TAT0−TA)=−kt1⇒kt1=−ln(350−300400−300)
⇒kt1=ln(2) ... (i)
In the second part (>t1) , body X cools by radiation (according to Newton’s law) as well as by conduction.
Therefore, rate of cooling = (cooling by radiation) + (cooling by conduction)

In conduction ,dQdt=KA(T−TA)L=C(−dTdt)∴(−dTdt)=KALC(T−TA)
where, C = heat capacity of body X
∴(−dTdt)=k(T−TA)+KACL(T−TA)... (ii)
(−dTdt)=(k+KACL)(T−TA)...(iii)
Let at t=3t1 , temperature of x becomes T2
Then from Eq. (iii)
∫T2T1dTT−TA=−(k+KAKC)∫3t1t1dt
ln(T2−TAT1−TA)=−(k+KALC)(2t1)=−(2kt1+2KALCt1)
orln(T2−300350−300)=−2ln(2)−2KAt1LC,kt1=ln(2) from Eq . (i) .
This equation gives T2=(300+12.5e−2KAt1CL)K

Similar Questions
A solid body A of mass m and specific heat capacity ‘s’ has temperature T1=400K. It is placed, at time t=0, in atmosphere having temperature T0=300K. It cools, following Newton’s law of cooling and its temperature was found to be T2=350Kat time t0. At time t0, the body A is connected to a large water bath maintained at atmospheric temperature T0, using a conducting rod of length L, cross section A and thermal conductivity k. The cross sectional area A of the connecting rod is small compared to the overall surface area of body A. Find the temperature of A at time t=2t0.
View SolutionTwo identical rods AB and CD, each of length L are connected as shown in figure-4.22. Their cross-sectional area is A and their thermal conductivity is k. Ends A, C and D are maintained at temperatures T1,T2andT3 respectively. Neglecting heat loss to the surroundings, find the temperature at B.
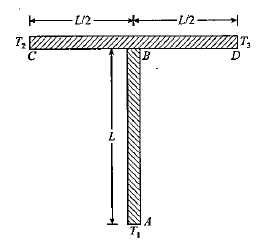
View Solution
Knowledge Check
A body at temperature 310 K is kept in an atmosphere whose temperature is 300 K. The temperature versus time graph of the body will be
A B
B C
C Dnone of the above
Dnone of the aboveA liquid in a beaker has temperature θ(t) at time t and θ0 is temperature of surroundings, then according to Newton's law of cooling the correct graph between loge(θ−θ0) and t is :
A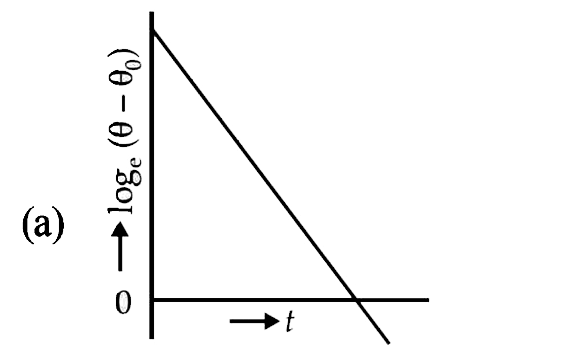 B
B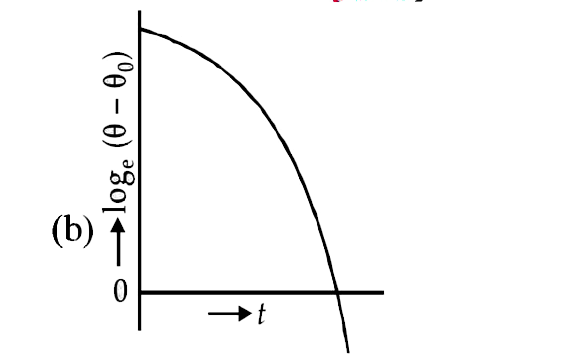 C
C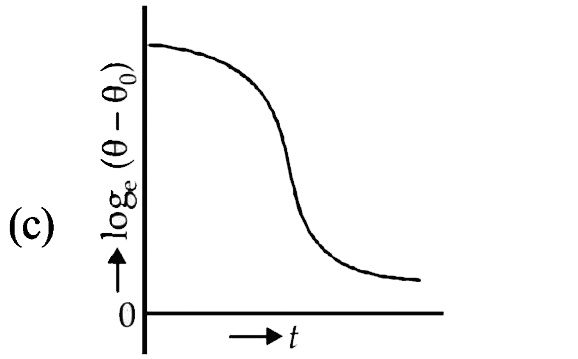 D
D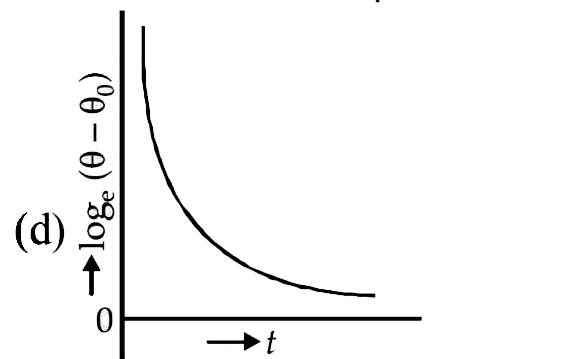
A body cools from a temperature 3T to 2T in 10 minutes. The room temperature is T. Assume that Newton's law of cooling is applicable. The temperature of the body at the end of next 10 minutes will be
A43TBTC74TD32T
Two bodies of masses m1 and m2 and specific heat capacities S1 and S2 are connected by a rod of length l, cross-ssection area A, thermal conductivity K and negligible heat capacity. The whole system is thermally insulated. At time t=0 , the temperature of the fisrt body is T1 and the temperature of the second body is T2(T2>T1) . Find the temperature difference between the two bodies at time t.
View SolutionA rod of length l and cross sectional area A has a variable conductivity given by K=αT, where α is a positive constant T is temperatures in Kelvin. Two ends of the rod are maintained at temperatures T1 and T2(T1>T2). Heat current flowing through the rod will be
View SolutionA solid at temperature T1 is kept in an evacuated chamber at temperature T2>T1 . The rate of increase of temperature of the body is propertional to
View SolutionA rod of length l and cross-section area A has a variable thermal conductivity given by K = α T, where α is a positive constant and T is temperature in kelvin. Two ends of the rod are maintained at temperature T1 and T2 (T1>T2). Heat current flowing through the rod will be
View SolutionOne end of a thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two sections of length l1andl2 and thermal conductivities K1andK2 respectively. The temperature at the interface of the two section is
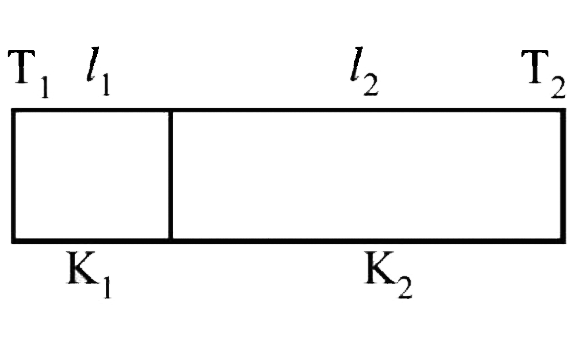
View Solution
