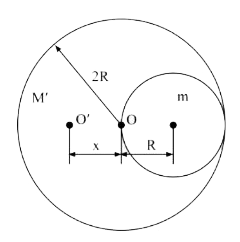
A circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumferences of the discs coincide. The center of mass of new disc is αR from the center of the bigger disc. The value of α is
1/2
1/6
1/4
1/3
The correct Answer is:D
Let after cutting the disc of radius R, the mass of remaining disc be and mass of removed disc be m.
Let (M'+m)=M=π(2R)2.σ=4πR2.σ
(Where σ is mass per unit area)
∵m=πR2.(−σ)∵M'=(4πR2⋅σ)−(πR2⋅σ)=3πR2⋅σ
For full disc, the centre of mass is at the centre O. After removing the disc of radius R let centre of mass shift by distance x.
∴x=4πR2σ.0−πR2σR4πR2.σ−πR2⋅σ=−R3⇒x=−R3=αR ∴ |α|=∣∣∣−13∣∣∣
The centre of mass is at R/3 to the left on the diameter of the original disc.
Similar Questions
A circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumference of the discs coincoid . The centre of mass of the new disc is αR from the centre of the bigger disc . the value of α is
View SolutionA solid toy is in the form of a hemisphere surmounted by a right circular cone of same radius. The height of the cone is 10 Cm and the radius of the base is 7 cm. Determine the volume of the toy. Also find the area of the coloured sheet required to cover the toy. (Use π=22/7 and √149=12.2)
View Solution
Knowledge Check
A circular disc of radius R is removed from a bigger circular disc of radius 2R such that the cirucmferences of the discs coincide. The centre of mass of the new disc is αR from the center of the bigger disc. The value of α is
A14B13C12D16A circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumference of the discs coincoid . The centre of mass of the new disc is αR from the centre of the bigger disc . the value of α is
A1/3B1/2C1/6D1/4A circular disc of radius R is removed from a bigger circular dise of radius such that the circumferences of the discs coincide. The centre of mass of the new disc is αR from the centre of the bigger disc. The value of a is:
A12B16C14D13
A circular disc of radius R is removed from a bigger circular disc of radius 2R, such that the circumference of the discs coincide. The centre of the bigger disc. The value of α is
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R, such that the circumference of the discs coincide. The centre of the bigger disc. The value of α is
View SolutionA circular disc of radius R is removed from a bigger of the discs coincide. The centre of mass of the new disc is ar from the centre of the bigger disc. The value of α is
View SolutionA circular disc of radius 20cm is cut from one edge of a larger circular disc of radius 50cm. The shift of centre of mass is
View SolutionFrom a circular disc of radius R, a square is cut out with a radius as its diagonal. The center of mass of remaining portion is at a distance from the center)
View Solution
