A sphere of mass m falls on a smooth hemisphere of mass M resting with its plane face on smooth horizontal table, so that at the moment of impact, line joining the centres makes an angle with the vertical. The velocity of sphere just before impact is u and e is the coefficient of restitution.
The velocity of hemisphere after impact will be zero
The hemisphere will move with a velocity v=musinαMcos2α
The hemisphere will move with a velocity v=mucosα(1+e)(M+m)
None of these
The correct Answer is:C
To solve the problem step by step, we will analyze the situation involving the sphere and the hemisphere, applying the principles of conservation of momentum and the coefficient of restitution.
Step 1: Analyze the Situation
We have a sphere of mass m falling towards a hemisphere of mass M. The line joining the centers of the sphere and the hemisphere makes an angle α with the vertical at the moment of impact. The velocity of the sphere just before impact is u.
Step 2: Resolve the Velocity of the Sphere
The velocity of the sphere can be resolved into two components:
- The component along the line joining the centers (which is the direction of impact):
ucosα
- The component perpendicular to the line joining the centers is not relevant for the collision analysis.
Step 3: Apply Conservation of Momentum
Let v be the velocity of the sphere after the impact and V be the velocity of the hemisphere after the impact. According to the conservation of momentum along the line joining the centers, we have:
mucosα=MV+mv
This is our first equation.
Step 4: Apply the Coefficient of Restitution
The coefficient of restitution e relates the relative velocities of separation and approach. The equation is given by:
e=Velocity of separationVelocity of approach
At the moment of impact, the velocity of approach is ucosα and the velocity of separation is V+v. Therefore, we can write:
V+v=eucosα
This is our second equation.
Step 5: Substitute and Solve for v
From the second equation, we can express v in terms of V:
v=eucosα−V
Now, substitute this expression for v into the first equation:
mucosα=MV+m(eucosα−V)
Expanding and rearranging gives:
mucosα=MV+meucosα−mV
mucosα−meucosα=(M−m)V
Factoring out ucosα:
ucosα(m−me)=(M−m)V
Thus,
V=ucosα(m(1−e))M−m
Step 6: Final Expression for v
Now, substituting V back into the expression for v:
v=eucosα−ucosα(m(1−e))M−m
This gives us the final expression for the velocities after the impact.
Final Result
The velocities after the impact can be expressed as:
V=mucosα(1+e)M+m
We have a sphere of mass m falling towards a hemisphere of mass M. The line joining the centers of the sphere and the hemisphere makes an angle α with the vertical at the moment of impact. The velocity of the sphere just before impact is u.
The velocity of the sphere can be resolved into two components:
- The component along the line joining the centers (which is the direction of impact):
ucosα
- The component perpendicular to the line joining the centers is not relevant for the collision analysis.
Let v be the velocity of the sphere after the impact and V be the velocity of the hemisphere after the impact. According to the conservation of momentum along the line joining the centers, we have:
mucosα=MV+mv
This is our first equation.
The coefficient of restitution e relates the relative velocities of separation and approach. The equation is given by:
e=Velocity of separationVelocity of approach
At the moment of impact, the velocity of approach is ucosα and the velocity of separation is V+v. Therefore, we can write:
V+v=eucosα
This is our second equation.
From the second equation, we can express v in terms of V:
v=eucosα−V
Now, substitute this expression for v into the first equation:
mucosα=MV+m(eucosα−V)
Expanding and rearranging gives:
mucosα=MV+meucosα−mV
mucosα−meucosα=(M−m)V
Factoring out ucosα:
ucosα(m−me)=(M−m)V
Thus,
V=ucosα(m(1−e))M−m
Now, substituting V back into the expression for v:
v=eucosα−ucosα(m(1−e))M−m
This gives us the final expression for the velocities after the impact.
The velocities after the impact can be expressed as:
V=mucosα(1+e)M+m
Similar Questions
A smooth wedge of mass M is kept at rest on a smooth horizontal surface . Inclined face of the wedge make an angle θ with the horizontal . A particle of mass m collides normal to inclined face of wedge . If speed of the particle just before collision is u and coefficient of restitution is e then find velocity of wedge after collision .
View SolutionA sphere of mass m, impinges obliquely on a sphere, of mass M, which is at rest. Show that, if m=eM, the directions of motion of the sphere after impact are at right angles.
View Solution
Knowledge Check
Two equal spheres of mass m are in contact on a smooth horizontal table. A third identical sphere impinges symmetrically on them and reduces to rest. Then:
 ACoefficient of restitution is e=23BLoss of kinetic energy 16mu2 where u is velocity before impactCAfter the collision, velocity of equal mass sphere is u√3DLoss of kinetic energy 13mu2
ACoefficient of restitution is e=23BLoss of kinetic energy 16mu2 where u is velocity before impactCAfter the collision, velocity of equal mass sphere is u√3DLoss of kinetic energy 13mu2A sphere of mass m moving with velocity v collides head -on on another sphere of same mass which is at rest. The ratio of final velocity of second sphere to the initial velocity of the first sphere is (where, e is coefficient of restitution and collision is inelastic)
Ae−12Be2Ce+12DeA sphere of mass 'm' moving with velocity 'v' collides head-on on another sphere of same mass which is at rest. The ratio of final velocity of second sphere to the initial velocity of the first sphere is (e is coefficient of restitution and collision is inelastic)
Ae−12Be2Ce+12De
A ball of mass m is projected vertically up from a smooth horizontal floor with a speed v. Find the total momentum delivered by the ball to the surface during impact assuming e as the cofficient of restitution of impact.

View SolutionA smooth hemisphere of mass m and radius R is at rest. A smooth solid sphere of mass 2m and radius R moving with velocity V0 between two horizontal smooth surfaces separated by a distance slightly greater than 2R as shown in figure. Solid sphere collides with the hemisphere. if coefficient of restitution is 12, then

View SolutionA solid sphere of mass M and radius R is placed on a smooth horizontal surface. It is given a horizontal impulse J at a height h above the centre of mass and sphere starts rolling then, the value of h and speed of centre of mass are –
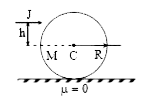
View SolutionA uniform solid sphere of mass M and radius R is placed on a smooth horizontal surface. It is given a horizontal impulse J at a height h above the centre of mass and sphere starts rolling. Then the value of h and speed of ccentre of mass are
View SolutionA sphere of mass m moving with a velocity u hits another stationary sphere of same mass. If e is the coefficient of restitution, what is the ratio of the velocities of two spheres after the collision?
View Solution
