A car of mass M is accelerating on a level smooth road under the action of a single force F acting along the direction of motion. The power delivered to the car is constant and equal to p. If the velocity of the car at an instant is v, then after travelling a distance of 7Mv33p the velocity become kv where k is__________.
The correct Answer is:2
To solve the problem step by step, we will analyze the given information and derive the necessary equations to find the value of k.
Step 1: Understand the relationship between power, force, and velocity
The power P delivered to the car is given by the equation:
P=F⋅v
where F is the force acting on the car and v is its velocity.
Step 2: Relate force to mass and acceleration
According to Newton's second law, the force can also be expressed as:
F=M⋅a
where a is the acceleration of the car. The acceleration can be expressed in terms of velocity and displacement:
a=dvdt=vdvdx
Substituting this into the force equation gives:
F=M⋅vdvdx
Step 3: Substitute into the power equation
Substituting F into the power equation:
P=M⋅vdvdx⋅v=M⋅v2dvdx
Step 4: Rearranging the equation
Rearranging gives:
dvdx=PM⋅v2
Step 5: Integrate both sides
We need to integrate both sides with respect to x. The left side will be integrated from v to kv and the right side from 0 to s:
∫kvvdv=∫s0PM⋅v2dx
Step 6: Calculate the integrals
The left side gives:
∫kvvdv=kv−v=(k−1)v
The right side becomes:
∫s0PM⋅1v2dx=PM⋅s
Step 7: Substitute the given distance
We know that s=7Mv33P. Substituting this into the equation gives:
(k−1)v=PM⋅7Mv33P
Simplifying this:
(k−1)v=7v33
Step 8: Solve for k
Dividing both sides by v (assuming v≠0):
k−1=7v23
Thus,
k=1+7v23
Step 9: Find the value of k
To find k, we need to express it in terms of a constant. From the earlier analysis, we can derive that:
k3−1=7⟹k3=8⟹k=2
Final Answer
Thus, the value of k is:
2
The power P delivered to the car is given by the equation:
P=F⋅v
where F is the force acting on the car and v is its velocity.
According to Newton's second law, the force can also be expressed as:
F=M⋅a
where a is the acceleration of the car. The acceleration can be expressed in terms of velocity and displacement:
a=dvdt=vdvdx
Substituting this into the force equation gives:
F=M⋅vdvdx
Substituting F into the power equation:
P=M⋅vdvdx⋅v=M⋅v2dvdx
Rearranging gives:
dvdx=PM⋅v2
We need to integrate both sides with respect to x. The left side will be integrated from v to kv and the right side from 0 to s:
∫kvvdv=∫s0PM⋅v2dx
The left side gives:
∫kvvdv=kv−v=(k−1)v
The right side becomes:
∫s0PM⋅1v2dx=PM⋅s
We know that s=7Mv33P. Substituting this into the equation gives:
(k−1)v=PM⋅7Mv33P
Simplifying this:
(k−1)v=7v33
Dividing both sides by v (assuming v≠0):
k−1=7v23
Thus,
k=1+7v23
To find k, we need to express it in terms of a constant. From the earlier analysis, we can derive that:
k3−1=7⟹k3=8⟹k=2
Thus, the value of k is:
2
Similar Questions
A car of mass one metric ton travels along a horizontal straight road with its engine working at a constant rate of 20kW. The resistance to motion of the card is 600N. Find the acceleration of the car at an instant, when its speed is 25 m/s
View SolutionA car of mass m starts from rest and accelerates so that the instantaneous power delivered to the car has a constant magnitude P0. The instantaneous velocity of this car is proportional to
View Solution
Knowledge Check
A car of mass m is accelerating on a level smooth road under the action of a single F. The power delivered to the car is constant and equal to P. If the velocity of the car at an instant is v, then after travelling how much distance it becomes double?
 . A(a) 7mv33PB(b) 4mv33PC(c) mv3PD(d) 18mv37P
. A(a) 7mv33PB(b) 4mv33PC(c) mv3PD(d) 18mv37PA car (treat it as particle) of mas 'm' is accelerating on a level smooth roud under the action of single force F. The power dellvered to the car is constant and equal to P. If the velocity of the car at an instant is v, then after traveclling how much distance it becomes double ?
 A7mv33pB4mv33pCmv3PD18mv37P
A7mv33pB4mv33pCmv3PD18mv37PA car of mass m starts from rest and accelerates so that the instantaneous power delivered to the car has a constant magnitude P0. The instantaneous velocity of this car is proportional to
At2P0Bt1/2Ct−1/2Dt/√m
A car of mass m is driven with acceleration a along a straight level road against a constant external resistive force R. When the velocity of the car V, the rate at which the engine of the car is doing work will be
View SolutionA car of mass m is driven with acceleration a along a straight level road against a constant external resistive force R. When the velocity of the car V, the rate at which the engine of the car is doing work will be
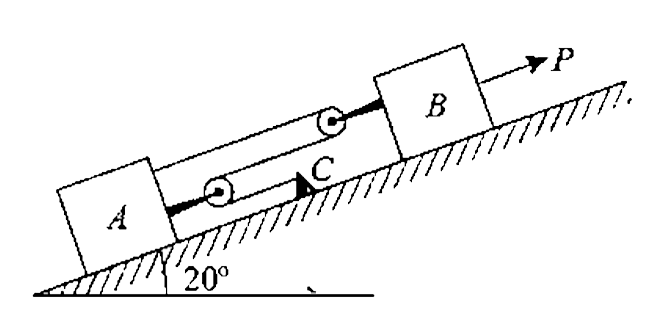
View SolutionUnder the action of force P, the constant acceleration of block B is 6m/sec2 up the incline. For the instant when the velocity of B is 3m/sec up the incline. Choose the correct option(s)
View SolutionA car travelling along a road begins accelerating with a constant acceleration of 1.5m/s2 in the direction of motion. After travelling 392 m at this acceleration, its speed is 35 m/s. Determine the speed of the car when it began accelerating.
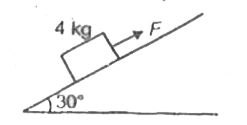
View SolutionA block of mass 4 kg is pulled along a smooth inclined plane of inclination 30∘ with constant velocity 3 m/s as shown, power delivered by the force is
View Solution

