A car travelling along a road begins accelerating with a constant acceleration of 1.5m/s2 in the direction of motion. After travelling 392 m at this acceleration, its speed is 35 m/s. Determine the speed of the car when it began accelerating.
1.5 m/s
34 m/s
7.0 m/s
49 m/s
The correct Answer is:C
To determine the speed of the car when it began accelerating, we can use the equations of motion. Here's a step-by-step solution:
Step 1: Identify the known values
- Final velocity (V) = 35 m/s (the speed after acceleration)
- Acceleration (a) = 1.5 m/s²
- Distance travelled during acceleration (s) = 392 m
Step 2: Use the equation of motion
We will use the third equation of motion, which relates initial velocity (u), final velocity (V), acceleration (a), and distance (s):
V2=u2+2as
Step 3: Rearrange the equation to solve for initial velocity (u)
Rearranging the equation gives:
u2=V2−2as
Step 4: Substitute the known values into the equation
Substituting the known values into the equation:
- V = 35 m/s
- a = 1.5 m/s²
- s = 392 m
So we have:
u2=(35)2−2×(1.5)×(392)
Step 5: Calculate the values
Calculating (35)2:
(35)2=1225
Calculating 2×(1.5)×(392):
2×1.5=3
3×392=1176
Now substituting these values back into the equation:
u2=1225−1176
u2=49
Step 6: Solve for u
Taking the square root of both sides:
u=√49
u=7m/s
Conclusion
The speed of the car when it began accelerating was 7 m/s.
---
- Final velocity (V) = 35 m/s (the speed after acceleration)
- Acceleration (a) = 1.5 m/s²
- Distance travelled during acceleration (s) = 392 m
We will use the third equation of motion, which relates initial velocity (u), final velocity (V), acceleration (a), and distance (s):
V2=u2+2as
Rearranging the equation gives:
u2=V2−2as
Substituting the known values into the equation:
- V = 35 m/s
- a = 1.5 m/s²
- s = 392 m
u2=(35)2−2×(1.5)×(392)
Calculating (35)2:
(35)2=1225
2×1.5=3
3×392=1176
u2=1225−1176
u2=49
Taking the square root of both sides:
u=√49
u=7m/s
The speed of the car when it began accelerating was 7 m/s.
Topper's Solved these Questions
- MOTION ALONG A STRAIGHT LINEBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( More than One Correct Choice Type )
6 Videos
- MOTION ALONG A STRAIGHT LINEBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Linked Comprehension )
15 Videos
- MOTION ALONG A STRAIGHT LINEBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PROBLEMS
53 Videos
- MAGNETIC FORCEBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Practice Questions (Integer type )
7 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)
10 Videos
Similar Questions
A car is travelling along the road at 8 m s−1. It accelerates at 1 m s−2 for a distance of 18 m. How fast is it then travelling ?
View SolutionA car starts accelerating with an acceleration of 13m/s2 when its speed was 18km/h. If the desplacement of car in nth minute after it starts accelerating is 4.8km then n is :
View Solution
Knowledge Check
A trolley moves down a slope from rest with constant acceleration. In the first second of its motion it travels 1.6 m. Its acceleration (in m/s2) is
A3.2B1.6C0.8D2.4At t=0 and x=0 , an initially stationary blue car begins to accelerate at a constant rate of 2.0m/s2 in the positive direction of the x -axis At =t = 2s a red car travelling in an adjecent lane and in the same direction passes x =0 with a speed of 8.0m/s and a constant accleration of 3.0m/s2 .the time when red car passes the blue car is :
A4.2 sB3.6 sC2.9 sDNone of theseA car is travelling on a circular banked road. The centripetal accelerations of a car is provided by
Anormal reactionBweight of a carChorizontal component of normal reactionDvertical component of normal reaction
The brakes applied to a car produce an acceleration of 6m/s2 in the opposite direction to the motion . If the car takes 2s to stop after the application of brakes , calculate the distance it travels during this time.
View SolutionThe jet plane starts from rest at s=0 and is subjected to the acceleration shown. Determine the speed of the plane when it has travelled 60 m.
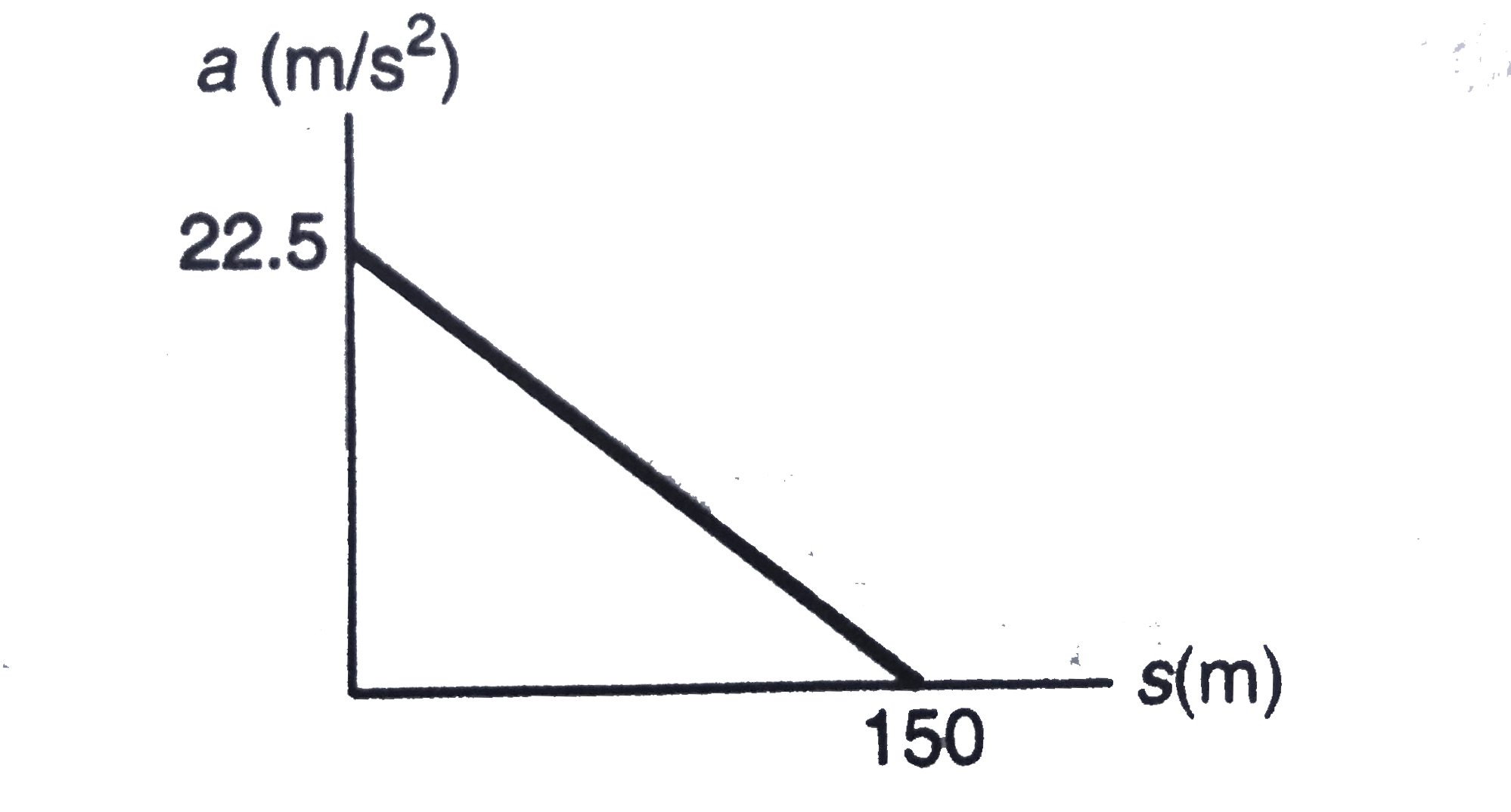
View SolutionThe retarding acceleration of 7.35ms−2 due to frictional force stops the car of mass 400 kg travelling in a road. Then, the coefficient of friction between the tyre of the car and the road, is__.
View SolutionA car moving on a straight road accelerated from a speed of 4.1m/s to a speed of 6.9m/s in 5.0 s. Then its average acceleration is
View SolutionA motor car moving with a uniform speed of 20m/sec comes to stop on the application of brakes after travelling a distance of 10m Its acceleration is
View Solution
