The coefficient of viscosity (η) of a fluid moving steadily between two surface is given by the formula (f)=ηAdV/dx where f is the frictional force on the fluid, A is the area in the fluid, and dV/dx is velocity gradient inside the fluid at that area. The SI unit of viscosity is given as :
kgm−1s−1
Nm−2s
Nil
Newtons
The correct Answer is:B
is the correct answer.
Related Playlists
- BOOK - DINESH PUBLICATIONCHAPTER - STATES OF MATTER : GASES AND LIQUIDSEXERCISE - Select the correct answer34videos
STATES OF MATTER : GASES AND LIQUIDS
- BOOK - DINESH PUBLICATIONCHAPTER - STATES OF MATTER : GASES AND LIQUIDSEXERCISE - Comphension 15videos
STATES OF MATTER : GASES AND LIQUIDS
- BOOK - DINESH PUBLICATIONCHAPTER - STATES OF MATTER : GASES AND LIQUIDSEXERCISE - Very Short Answer Questions25videos
STATES OF MATTER : GASES AND LIQUIDS
- BOOK - DINESH PUBLICATIONCHAPTER - STATES OF MATTER (SOLID STATE CHEMISTRY)EXERCISE - ULTIMATE PREPARATORY PACKAGE21videos
STATES OF MATTER (SOLID STATE CHEMISTRY)
- BOOK - DINESH PUBLICATIONCHAPTER - STRUCTURE OF ATOMEXERCISE - Reason Type Questions1videos
STRUCTURE OF ATOM
Similar Questions
The coefficient of viscosity (η) of a fluid moving steadily between two surface is given by the formula (f)=ηAdV/dx where f is the frictional force on the fluid, A is the area in the fluid, and dV/dx is velocity gradient inside the fluid at that area. The SI unit of viscosity is given as :
View SolutionThe coefficient of viscosity n of a fluid moving steadily between two surfaces is given by the formula, f=nAdVdx
where f is the frictional force on the fluid, A is an area in the fluid and dV/dx is the velocity gradient inside the fluid at that area. The SI unit of viscosity coefficient n is given as.View SolutionWhen a liquid flows in a tube, there is relative motion between adjacent layers of the liquid. This force is called the viscous force which tends to oppose the relative motion between the layers of the liquid. Newton was the first person to study the factors that govern the viscous force in a liquid. According to Newton’s law of viscous flow, the magnitude of the viscous force on a certain layer of a liquid is given by
F=−ηAdvdx
where A is the area of the layer dvdx is the velocity gradient at the layer and η is the coefficient of viscosity of the liquid.
The dimensional formula for the coefficient of viscosity is :View SolutionWhen a liquid flows in a tube, there is relative motion between adjacent layers of the liquid. This force is called the viscous force which tends to oppose the relative motion between the layers of the liquid. Newton was the first person to study the factors that govern the viscous force in a liquid. According to Newton’s law of viscous flow, the magnitude of the viscous force on a certain layer of a liquid is given by
F=−ηAdvdx
where A is the area of the layer dvdx is the velocity gradient at the layer and η is the coefficient of viscosity of the liquid.
A river is 5 m deep. The velocity of water on its surface is 2ms−1 If the coefficient of viscosity of water is 10−3Nsm−2 , the viscous force per unit area is :View SolutionWhen a liquid flows in a tube, there is relative motion between adjacent layers of the liquid. This force is called the viscous force which tends to oppose the relative motion between the layers of the liquid. Newton was the first person to study the factors that govern the viscous force in a liquid. According to Newton’s law of viscous flow, the magnitude of the viscous force on a certain layer of a liquid is given by
F=−ηAdvdx
where A is the area of the layer dvdx is the velocity gradient at the layer and η is the coefficient of viscosity of the liquid.
If f is the frictional force between a solid sliding over another solid, and F is the viscous force when a liquid layer slides over another, then :View SolutionViscous force is represented as F=ηAdvdx. Where,η is proportionaly constant called as
View SolutionThe velocity distribution for the flow of a Newtonian fluid between two wide, parallel plates is given by the equation
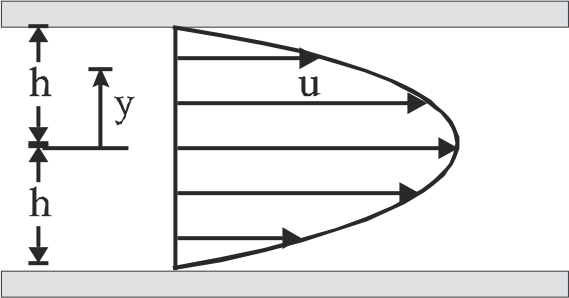
u=3V2[1−(yh)2]
where V is the mean velocity. The fluid has coefficient of viscosity η Answer the following 3 questions for this situation.
View SolutionA liquid whose coefficient of viscosity is η flows on a horizontal surface. Let dx represent the vertical distance between two layers of liquid and dv represent the difference in the velocities of the two layers. Then the quantity η(dv/dx) has the same dimensions as:
View SolutionWhen a viscous liquid flows , adjacent layers oppose their relative motion by applying a viscous force given by
F=−ηAdvdz
where , ete = coefficient of viscosity ,
A = surface area of adjacent layers in contact ,
dvdz = velocity gradient
Now , a viscous liquid having coefficient of viscosity η is flowing through a fixed tube of length l and radius R under a pressure difference P between the two ends of the tube . Now consider a cylindrical vloume of liquid of radius r . Due to steady flow , net force on the liquid in cylindrical volume should be zero .
−η2πrldvdr=Pπr2
−∫0v,dv=P2ηl∫Rτrdr(∵ layer in contact with the tube is stationary )
v=v0(1−r2R2) , where v0=PR24nl
∴ Q=πPR48stal
This is called Poisecuille's equation .

The velocity of flow of liquid at r = R/2 isView SolutionWhen a viscous liquid flows , adjacent layers oppose their relative motion by applying a viscous force given by
F=−ηAdvdz
where , ete = coefficient of viscosity ,
A = surface area of adjacent layers in contact ,
dvdz = velocity gradient
Now , a viscous liquid having coefficient of viscosity η is flowing through a fixed tube of length l and radius R under a pressure difference P between the two ends of the tube . Now consider a cylindrical vloume of liquid of radius r . Due to steady flow , net force on the liquid in cylindrical volume should be zero .
−η2πrldvdr=Pπr2
−∫0v,dv=P2ηl∫Rτrdr(∵ layer in contact with the tube is stationary )
v=v0(1−r2R2), where v0=PR24nl
∴ Q=πPR48stal
This is called Poisecuille's equation .

The viscous force on the cylindrical volume of the liquid varies asView Solution


