A liquid whose coefficient of viscosity is η flows on a horizontal surface. Let dx represent the vertical distance between two layers of liquid and dv represent the difference in the velocities of the two layers. Then the quantity η(dv/dx) has the same dimensions as:
Acceleration
Force
Momentum
Pressure
The correct Answer is:D
To solve the problem, we need to determine the dimensions of the quantity η(dvdx) where η is the coefficient of viscosity, dv is the difference in velocities between two layers of liquid, and dx is the vertical distance between those layers.
1. Identify the dimensions of the coefficient of viscosity η:
- The coefficient of viscosity η is defined as the ratio of shear stress to the shear rate.
- Shear stress has dimensions of pressure, which is given by:
Dimensions of pressure=ForceArea=MLT−2L2=ML−1T−2
- Shear rate is defined as the velocity gradient, which has dimensions of:
Dimensions of shear rate=VelocityDistance=LT−1L=T−1
- Therefore, the dimensions of viscosity η can be calculated as:
η=Shear stressShear rate=ML−1T−2T−1=ML−1T−1
2. Determine the dimensions of dvdx:
- Here, dv represents the difference in velocities, which has dimensions of:
Dimensions of velocity=LT−1
- The distance dx has dimensions of:
Dimensions of distance=L
- Therefore, the dimensions of dvdx are:
dvdx=LT−1L=T−1
3. Combine the dimensions of η and dvdx:
- Now we can find the dimensions of the product η(dvdx):
Dimensions of η(dvdx)=(ML−1T−1)(T−1)=ML−1T−2
4. Compare with known dimensions:
- The dimensions ML−1T−2 correspond to the dimensions of pressure.
Conclusion:
The quantity η(dvdx) has the same dimensions as pressure.
- The coefficient of viscosity η is defined as the ratio of shear stress to the shear rate.
- Shear stress has dimensions of pressure, which is given by:
Dimensions of pressure=ForceArea=MLT−2L2=ML−1T−2
- Shear rate is defined as the velocity gradient, which has dimensions of:
Dimensions of shear rate=VelocityDistance=LT−1L=T−1
- Therefore, the dimensions of viscosity η can be calculated as:
η=Shear stressShear rate=ML−1T−2T−1=ML−1T−1
- Here, dv represents the difference in velocities, which has dimensions of:
Dimensions of velocity=LT−1
- The distance dx has dimensions of:
Dimensions of distance=L
- Therefore, the dimensions of dvdx are:
dvdx=LT−1L=T−1
- Now we can find the dimensions of the product η(dvdx):
Dimensions of η(dvdx)=(ML−1T−1)(T−1)=ML−1T−2
- The dimensions ML−1T−2 correspond to the dimensions of pressure.
The quantity η(dvdx) has the same dimensions as pressure.
Similar Questions
A liquid having coefficient of viscosity 0.02 decapoise is filled in a container of cross-sectional area 20 m^2 viscous drag between two adjacent layers in flowing is 1 N, then velocity gradient is
View SolutionThe viscous force acting between two layers of a liquid is given by FA=ηdvdz. This F/A may be caled
View Solution
Knowledge Check
If η represents the coefficient of viscosity and T the surface tension. Then the dimensions of T/η are same as that of
AlengthBmassCtimeDspeedA thin horizontal movable plate P is separated from two fixed horizontal plates P1 and P2 by two highly viscous liquids of coefficient of viscosity η1 and η2 as shown, where η2=4η1. Area of contact of movable plate with each fluid is same. If the distance between two fixed plates is h, then the distance h1 of movable plate from upper fixed plate such that the movable plate can be moved with a constant velocity by applying a minimum constant horizontal force F on movable plate is (assume velocity gradient to be uniform in each liquid).
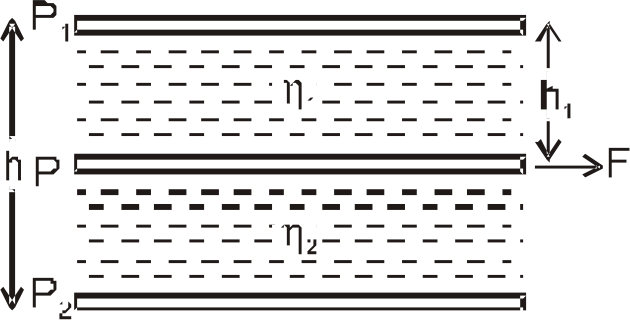 Ah/4Bh/2C2h/3Dh/3
Ah/4Bh/2C2h/3Dh/3A liquid flows through a horizontal tube. The velocities of the liquid in the two sections, which have areas of cross section A1 and A2 are v1 and v2 respectively. The difference in the levels of the liquid in the two vertical tubes is h. Then
 Athe volume of the liquid flowing through the tube in unit time is A1v1Bv2−v1=√2ghCv22−v21=2ghDthe energy per unit mass of the liquid is the same in both sections of the tube
Athe volume of the liquid flowing through the tube in unit time is A1v1Bv2−v1=√2ghCv22−v21=2ghDthe energy per unit mass of the liquid is the same in both sections of the tube
If a tangential force of 1dyne cm−2 of the surface is required to maintain a relative velocity of 1cms−1 between two layers of a liquid 1 cm apart, then the coefficient of viscosity of the liquid is said to be___.
View SolutionA liquid of density ρ and coefficient of viscosity η, flows with velocity υ through a tube of diameter D. A quantity R=ρυDη determines whether the flow will be streamlined or turbulent. R has the dimension of
View SolutionWhen a viscous liquid flows , adjacent layers oppose their relative motion by applying a viscous force given by
F=−ηAdvdz
where , ete = coefficient of viscosity ,
A = surface area of adjacent layers in contact ,
dvdz = velocity gradient
Now , a viscous liquid having coefficient of viscosity η is flowing through a fixed tube of length l and radius R under a pressure difference P between the two ends of the tube . Now consider a cylindrical vloume of liquid of radius r . Due to steady flow , net force on the liquid in cylindrical volume should be zero .
−η2πrldvdr=Pπr2
−∫0v,dv=P2ηl∫Rτrdr(∵ layer in contact with the tube is stationary )
v=v0(1−r2R2) , where v0=PR24nl
∴ Q=πPR48stal
This is called Poisecuille's equation .

The velocity of flow of liquid at r = R/2 is
View SolutionWhen a viscous liquid flows , adjacent layers oppose their relative motion by applying a viscous force given by
F=−ηAdvdz
where , ete = coefficient of viscosity ,
A = surface area of adjacent layers in contact ,
dvdz = velocity gradient
Now , a viscous liquid having coefficient of viscosity η is flowing through a fixed tube of length l and radius R under a pressure difference P between the two ends of the tube . Now consider a cylindrical vloume of liquid of radius r . Due to steady flow , net force on the liquid in cylindrical vloume should be zero .
−η2πrldvdr=Pπr2
−∫0v,dv=P2ηl∫Rτrdr(∵ layer in contact with the tube is stationary )
v=v0(1−r2R2), where v0=PR24nl
∴ Q=πPR48stal

This is called Poisecuille's equation .
The volume of the liquid flowing per sec across the cross - section of the tube is .
View SolutionWhen a viscous liquid flows , adjacent layers oppose their relative motion by applying a viscous force given by
F=−ηAdvdz
where , ete = coefficient of viscosity ,
A = surface area of adjacent layers in contact ,
dvdz = velocity gradient
Now , a viscous liquid having coefficient of viscosity η is flowing through a fixed tube of length l and radius R under a pressure difference P between the two ends of the tube . Now consider a cylindrical vloume of liquid of radius r . Due to steady flow , net force on the liquid in cylindrical volume should be zero .
−η2πrldvdr=Pπr2
−∫0v,dv=P2ηl∫Rτrdr(∵ layer in contact with the tube is stationary )
v=v0(1−r2R2), where v0=PR24nl
∴ Q=πPR48stal
This is called Poisecuille's equation .

The viscous force on the cylindrical volume of the liquid varies as
View Solution
