Find out the value of (P) in the following cycle:
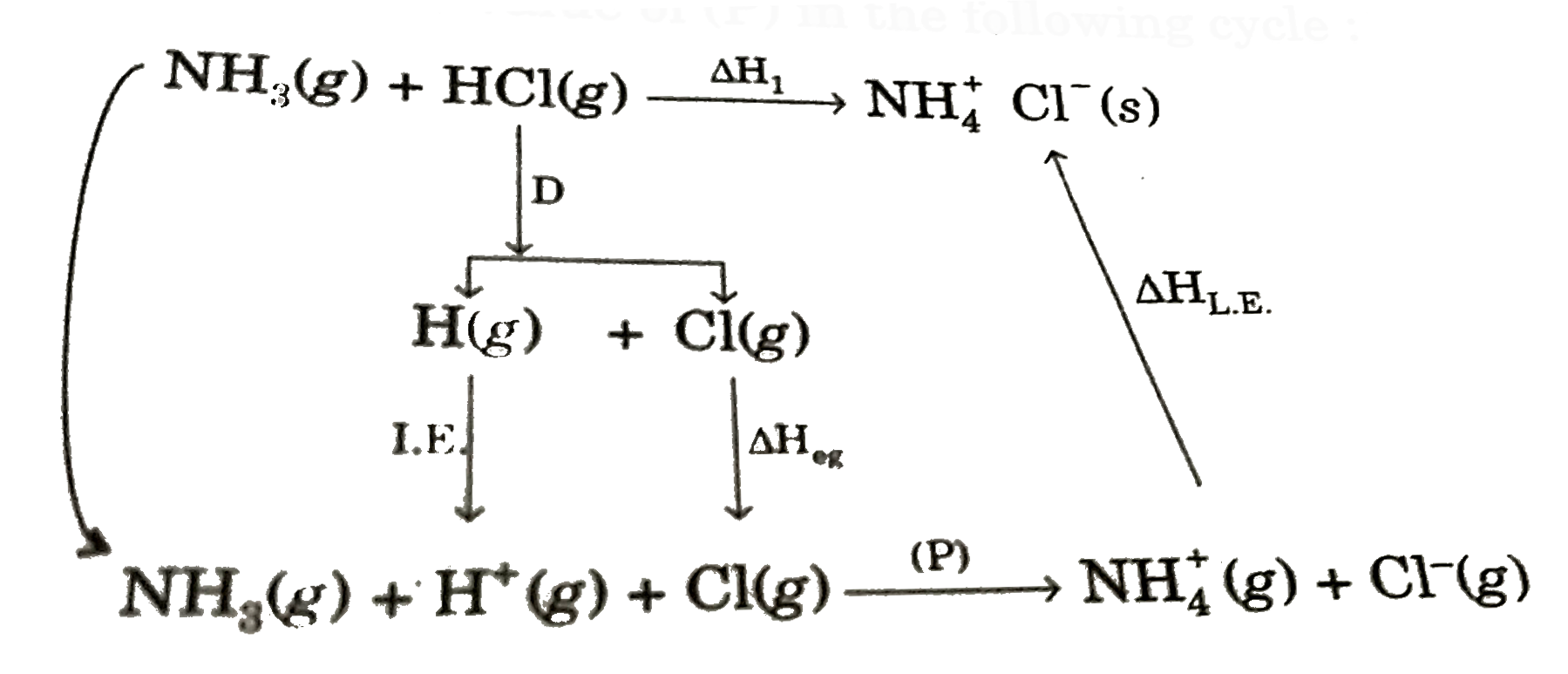
Given ΔH1=−400kJ,I.E.=+50kJ,D=+50kJ,ΔHeg=−30kJ lattice energy −−100kJ
−400kJ
−300kJ
−370kJ
−310kJ
The correct Answer is:C
ΔH1=D+IE+ΔHeg=P+ΔHL.E
Topper's Solved these Questions
- PERIODIC TABLEBook:GRB PUBLICATIONChapter:PERIODIC TABLEExercise:Reasoning Type
Explore 29 Videos
- PERIODIC TABLEBook:GRB PUBLICATIONChapter:PERIODIC TABLEExercise:Multiple Objective Type
Explore 64 Videos
- PERIODIC TABLEBook:GRB PUBLICATIONChapter:PERIODIC TABLEExercise:E.Electronegativity
Explore 54 Videos
- NOMENCLATURE AND CLASSIFICATIONBook:GRB PUBLICATIONChapter:NOMENCLATURE AND CLASSIFICATIONExercise:Subjective Type
Explore 24 Videos
- PRACTICAL ORGANIC CHEMISTRYBook:GRB PUBLICATIONChapter:PRACTICAL ORGANIC CHEMISTRYExercise:Exercise 4 (Matrix match type )
Explore 1 Video
Similar Questions
Find bond enthalpy of C=O (in kJ/mol) using following information :
ΔHatomisation[C(s)]=700 kJ/mol
ΔHf[CO2(g)]=−400 kJ/mol
BEo=o=500 kJ/mol
Resonance energy of CO2=−150 kJ/mol
View SolutionConsider the following process :-
A→2B,ΔH=+150KJ
3B→2C+D,ΔH=+350KJ
G+A→2D,ΔH=+350KJ
For B+D→G+2C,ΔH will be
View Solution
Knowledge Check
Following are the values of Ea and ΔH for three reactions carried out at the same temperature :
I:Ea=20kJmol−1,ΔH=−60kJmol−1
II : Ea=10kJmol−1,ΔH=−20kJmol−1
III: Ea=40kJmol−1,ΔH=+15kJmol−1
If all the three reaction have same frequency factor then fastest and slowest reations are :AFastestSlowestIIIBFastestSlowestIIIIICFastestSlowestIIIIDcan't be predictedGiven the following information :
A−(g)→A2+(g)+3e−ΔH1=1400KJ/mole
A(g)→A2+(g)+2e−ΔH2=700KJ/mole
ΔHeg[A+(g)]=−350KJ/mole
IE1+IE2 for A(g)=950KJ/mole
The value of IE1 of A− in KJ/mol is :A450B+350C+600D+250If bond energy of H2,F2 and HF are in the ratio 2:1:3 and ΔHa(H2)=400kJ/mol. Then ΔHf(HF) is :
A0kJ/molB−600kJ/molC−1200kJ/molDNone of these
Given the following information
A−(g)→A2+(g)+3e− ΔH1=1400kJmol−1
A(g)→A2+(aq)+2e− ΔH2=700kJmol−1
ΔHeg[A+(g)]=−350kJmol−1
where ΔHeg is electron gain enthalpy.
(IE1+IE2) for A(g)=950kJmol−1
The value of ΔHeg of A2+(g)in kJmol−1is
View SolutionGiven the following information
A−(g)→A2+(g)+3e− ΔH1=1400kJmol−1
A(g)→A2+(aq)+2e− ΔH2=700kJmol−1
ΔHeg[A+(g)]=−350kJmol−1
where ΔHeg is electron gain enthalpy.
(IE1+IE2) for A(g)=950kJmol−1
The value of ΔHeg of A2+(g)in kJmol−1is
View SolutionGiven the following information
A−(g)→A2+(g)+3e− ΔH1=1400kJmol−1
A(g)→A2+(aq)+2e− ΔH2=700kJmol−1
ΔHeg[A+(g)]=−350kJmol−1
where ΔHeg is electron gain enthalpy.
(IE1+IE2) for A(g)=950kJmol−1
The value of ΔHeg of A2+(g)in kJmol−1is
View SolutionFrom the following information
A−(g)→A+2(g)+3e−ΔH1=1400kJ/moleA(g)→A+2(aq)+2e−ΔH2=700kJ/moleΔHEG[A+(g)]=−350kJ/mol(IE1+IE2)forA(g)=950kJ/mol Find
(a) IE1 of A (b) IE2 of A (c) ΔHEG of A (d) ΔHHE of A^(2+)(g)
View SolutionGiven the following information
A−(g)→A2+(g)+3e− ΔH1=1400kJmol−1
A(g)→A2+(aq)+2e− ΔH2=700kJmol−1
ΔHeg[A+(g)]=−350kJmol−1
where ΔHeg is electron gain enthalpy.
(IE1+IE2) for A(g)=950kJmol−1
The value of IE1 of A− in kJ mol−1 is
View Solution

