If ABC is a right angled triangle with hypotenuse AB=P. Then $\to A B . \to A C + \to B C . \to B A + \to C A . \to C B = m p^{2}$ . Find m.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:1

$\to A B . \to A C + \to B C . \to B A + \to C A . \to C B = m p^{2}$
$p cos θ x (p sin θ) y θ = 90^{\circ}$
$p cos θ x + p sin θ y + - 0 m p^{2}$
$p cos θ . p cos θ + p sin θ - p sin θ = m p^{2}$

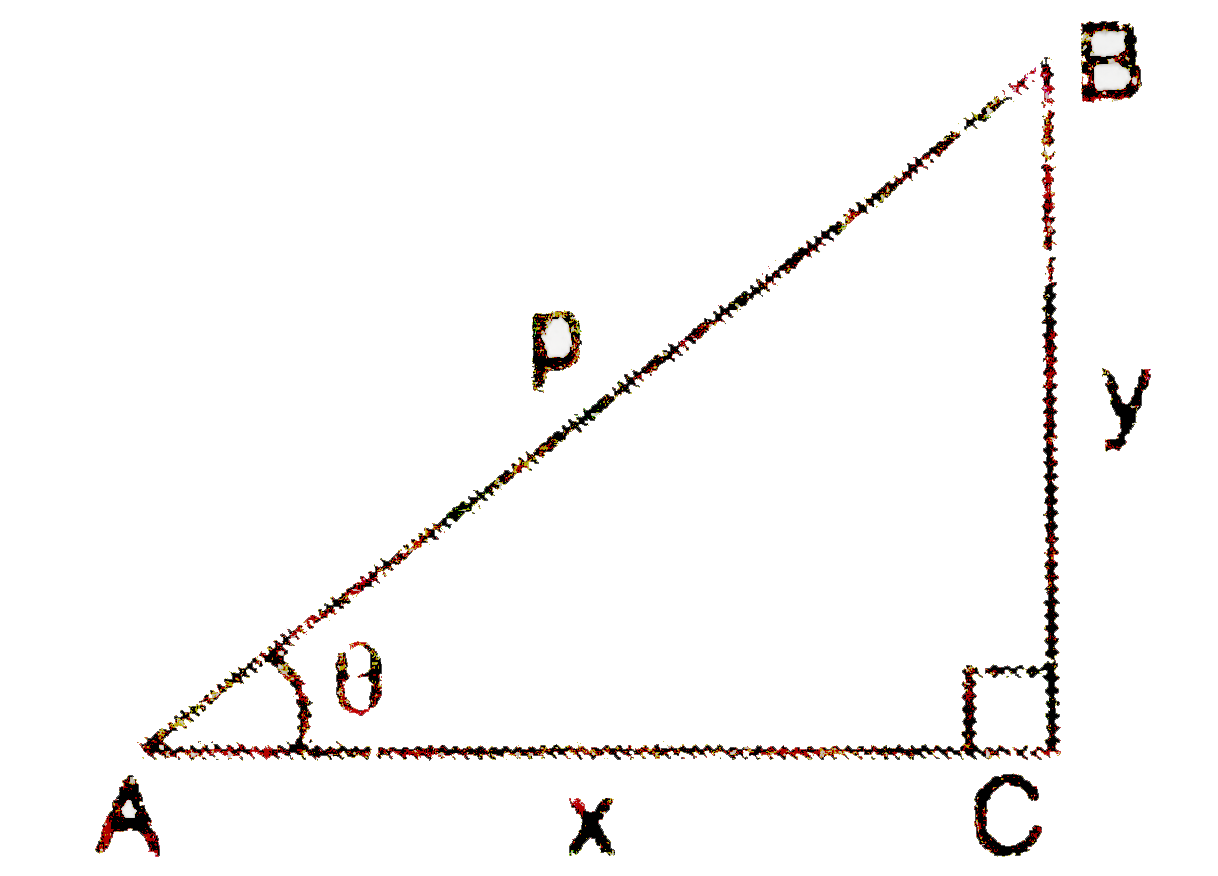
$p^{2} ({cos}^{2} θ + {sin}^{2} θ) = m p^{2}$
$m = 1$

|

Updated on:21/07/2023

Class 11 PHYSICS VECTOR

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In a right angled triangle ABC, the hypotenuse AB =p, then $- - \to A B . - - \to A C + - - \to B C . - - \to B A + - - \to C A . - - \to C B$ is equal to:
A $2 p^{2}$
B $p^{2} / 2$
C $p^{2}$
Dnone
Question 2 - Select One
In a right angled triangle ABC, the hypotenuse AB =p, then $- - \to A B . - - \to A C + - - \to B C . - - \to B A + - - \to C A . - - \to C B$ is equal to:
A $2 p^{2}$
B $\frac{p^{2}}{2}$
C $p^{2}$
DNone of these
Question 3 - Select One
If in a right-angled triangle ABC, hypotenuse AC=p, then what is $- - \to A B . - - \to A C + - - \to B C . - - \to B A + - - \to C A . - - \to C B$ equal to ?
A $p^{2}$
B $2 p^{2}$
C $\frac{p^{2}}{2}$
Dp

GRB PUBLICATION-VECTORS-INTERGER ANSWER

Home
Ask Doubt
Profile