Assertion: The minimum number of non-coplanar Vectors whose sum can be zero, is four
Reason: The resultant of two vectors of unequal magnitude can be zero.
A
2
B
3
C
4
D
6
Video Solution
Text Solution
The correct Answer is:B
→A+→B+→B=0
ABC is equilateral '∞'.
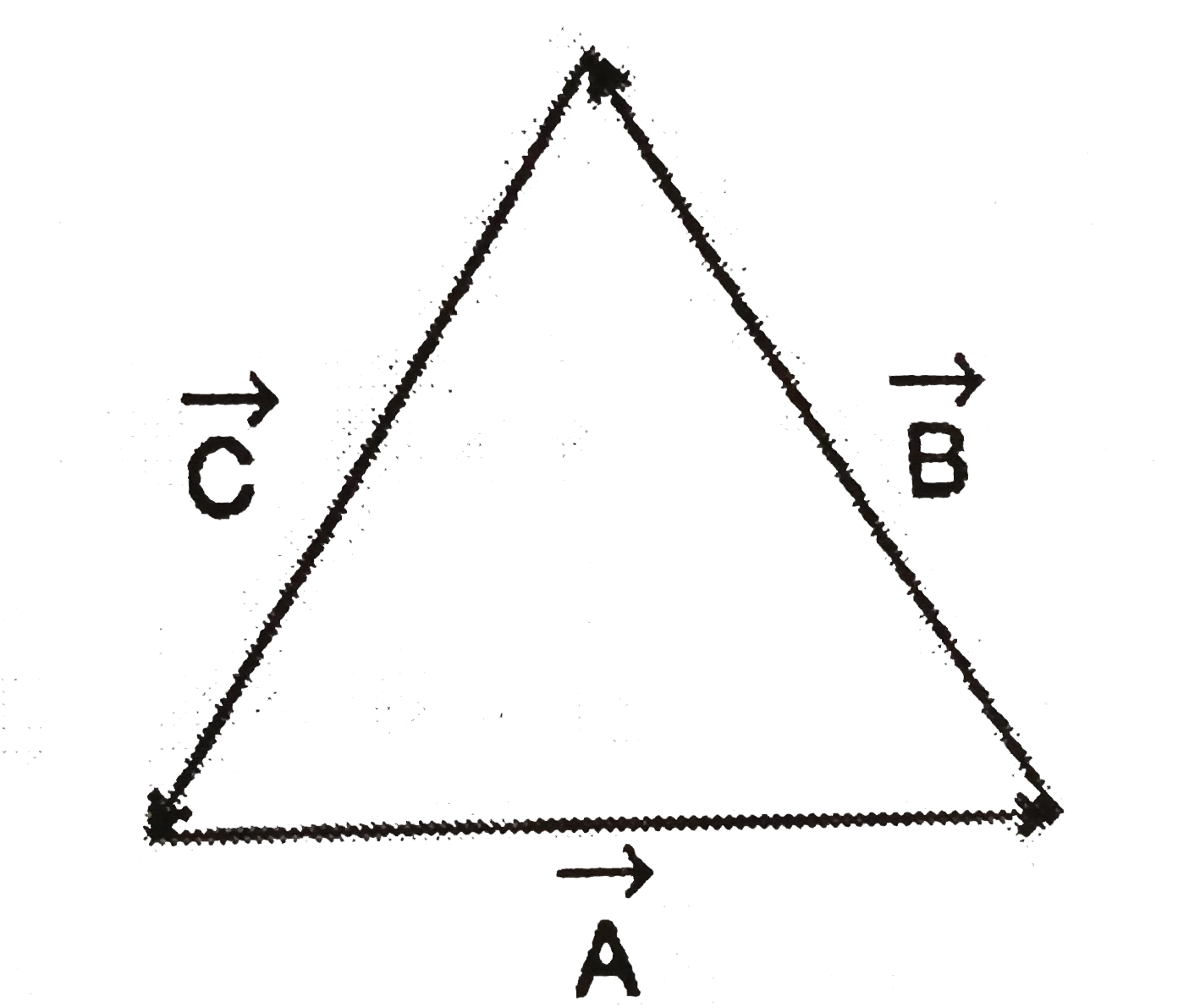
|
Topper's Solved these Questions
- VECTORSBook:GRB PUBLICATIONChapter:VECTORSExercise:MORE THAN ONE CHOICE IS CORRECT
Explore 15 Videos
- VECTORSBook:GRB PUBLICATIONChapter:VECTORSExercise:ASSERTION- REASON
Explore 1 Video
- VECTORSBook:GRB PUBLICATIONChapter:VECTORSExercise:PROBLEMS FOR PARCTICE
Explore 23 Videos
- UNITS AND DIMENSIONSBook:GRB PUBLICATIONChapter:UNITS AND DIMENSIONSExercise:Link Compression
Explore 6 Videos
Similar Questions
Knowledge Check
The minimum number of unequal vectors whose vector sum can be zero is
A1B2C3D4The minimum number of Non -zero vector is :
A3B2C4D1Can the resultant of two vectors be zero ?
ANoBYes, when the two vectors are equal in magnitude and directionCYes, when the two vectors are equal in magnitude but opposite in directionDYes, when the two vectors are equal in magnitude and making an anlge of 2π3 with each other
Assertion: The minimum number of vectors of unequal magnitude required to produce zero resultant is three.
Reason: Three vectors of unequal magnitude which can be represented by the three sides of a triangle taken in order, produce zero resultant.
View SolutionMinimum number of two coplanar vectors of equal magnitude whose vectors sum could be zero, is:
View SolutionThe minimum number of vector having different planes which can be added to give zero resultant is
View SolutionHow many minimum numbers of non zero vectors in different planes can be added to give zero resultant.
View SolutionHow many minimum numbers of a coplanar vector having different magntidues can be added to give zero resultant
View Solution

