ABCD is parallelogram →A,→B,→Cand→D are the position vectors of vecticles A, B, C, and D with respect to any origin, them:
→A+→B=→C−→D
→C−→B=→A+→D
→B−→C=→A−→D
→A+→B+→C+→D=0
The correct Answer is:C
→A→B+→C→D=0
(→B−→A)+→D−→C=0
Sum of opposite sides = zero
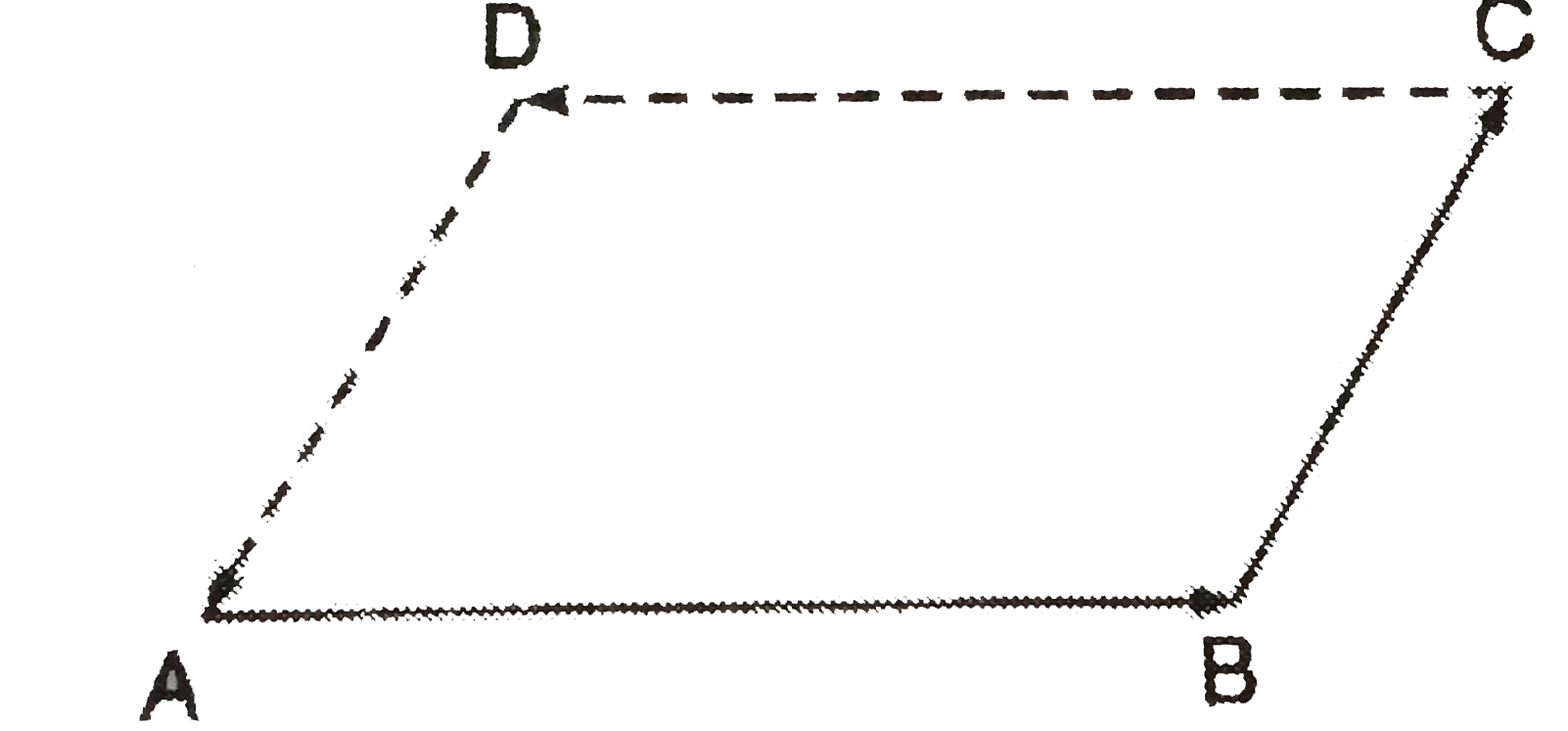
Topper's Solved these Questions
- VECTORSBook:GRB PUBLICATIONChapter:VECTORSExercise:MORE THAN ONE CHOICE IS CORRECT
Explore 15 Videos
- VECTORSBook:GRB PUBLICATIONChapter:VECTORSExercise:ASSERTION- REASON
Explore 1 Video
- VECTORSBook:GRB PUBLICATIONChapter:VECTORSExercise:PROBLEMS FOR PARCTICE
Explore 23 Videos
- UNITS AND DIMENSIONSBook:GRB PUBLICATIONChapter:UNITS AND DIMENSIONSExercise:Link Compression
Explore 6 Videos
Similar Questions
→a,→b,→c are the position vectors of vertices A, B, C respectively of a paralleloram, ABCD, ifnd the position vector of D.
View SolutionIf →a,→b,→c,→d are the position vectors of points A,B,CandD, respectively referred to the same origin O such that no three of these points are collinear and →a+→c=→b+→d, then prove that quadrilateral ABCD is a parallelogram.
View Solution
Knowledge Check
Let the position vectors of vertices A,B,C of ΔABC be respectively →a,→b and →c. If →r is the position vector of the mid point of the line segment joining its orthocentre and centroid then (→a−→r)+(→b−→r)+(→c−→r)=
A1B2C3Dnone of theseIf →A×→B=→C+→D, them select the correct alternative:
A→B is parallel to →C+→DB→A is perpendicular to →CCComponent of →C along →A = Components of →D along →ADComponent of →C along →A =-Components of →D along →AA, B, C and D have position vectors →a,→b,→cand→d, repectively, such that →a−→b=2(→d−→c). Then
AAB and CD bisect each otherBBD and AC bisect each otherCAB and CD trisect each otherDBD and AC trisect each other
In a ΔABC, the sides BC, CA and AB are consecutive positive integers in increasing order. Let →a,→band→c are position vectors of the vertices A, B and C respectively. If (→c−→a).(→b−→c)=0, then the value of ∣∣→a×→b+→b×→c+→c×→a∣∣ is equal to
View SolutionIf →a+2→b+3→c,2→a+→b+3→c,2→+5veb−→cand→a−→b−→c be the positions vectors A,B,C and D respectively, prove that −−→ABand−−→CD are parallel. Is ABCD a parallelogram?
View SolutionIf →a,→b,→cand→d are the position vectors of the vertices of a cycle quadrilateral ABCD, prove that ∣∣→a×→b+→b×→d+→d×→a∣∣(→b−→a).(→d−→a)+∣∣→b×→c+→c×→d+→d+→d×→b∣∣(→b−→c).(→d−→c)
View SolutionIf →a,→b,→cand→d are the position vectors of the vertices of a cycle quadrilateral ABCD, prove that ∣∣→a×→b+→b×→d+→d×→a∣∣(→b−→a).(→d−→a)+∣∣→b×→c+→c×→d+→d+→d×→b∣∣(→b−→c).(→d−→c)
View SolutionIf →a,→b,→c&→d are position vector of point A,B,C and D respectively in 3-D space no three of A,B,C,D are collinnear and satisfy the relation 3→a−2→b+→c−2→d=0 then
View Solution

