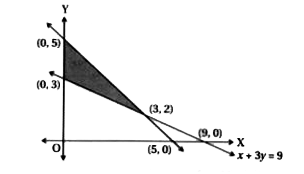
Find the optimal solution of the above LPP and also find the value of from the graph of feasible region Solution in Bengali
The correct Answer is:A, D
Step by step video, text & image solution for Find the optimal solution of the above LPP and also find the value of Z_(max) from the graph of feasible region by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR PROGRAMMING GRAPHICAL METHOD Book:CHHAYA PUBLICATIONChapter:LINEAR PROGRAMMING GRAPHICAL METHOD Exercise:Long Answer Type Question
Explore 16 Videos
- LINEAR PROGRAMMING GRAPHICAL METHOD Book:CHHAYA PUBLICATIONChapter:LINEAR PROGRAMMING GRAPHICAL METHOD Exercise:Multiple Correct Answers Type
Explore 5 Videos
- LINEAR PROGRAMMING GRAPHICAL METHOD Book:CHHAYA PUBLICATIONChapter:LINEAR PROGRAMMING GRAPHICAL METHOD Exercise:Very Short Answer Type Question
Explore 10 Videos
- LINEAR INEQUATIONSBook:CHHAYA PUBLICATIONChapter:LINEAR INEQUATIONSExercise:SAMPLE QUESTION FOR COMPETITIVE EXAMS (Assertion- Reason Type)
Explore 2 Videos
- LOGARITHM Book:CHHAYA PUBLICATIONChapter:LOGARITHM Exercise:Long Answer Type Question
Explore 12 Videos
Similar Questions
A company sells two different products P1 and P2 The company makes profits of Rs 40 and Rs 30 per unit on product P1 and P2 respectively. the two products are produced in a common production process and are sold in two different markets the production process has a capacity of 30000 men hours it takes 3 hours to produces one unit of P1 and 1 hour to produce one unit of P2 the market has been surveyed and company officals feels that the maximum number of P_(1) that can be sold is 8000 and maximum number that of P2 is 12000 units. formulate the above problem and solve it by graphical method
View SolutionA general linear programming problem is to maximize or minimize a function f= px +qy, p2+q2≠0 subject ot (i)x≥0,y≥0,(ii)a1x+b1y≥c1,(iii)a2x+b2y≤c2 etc then f and (i) (ii) , (iii) etc are defined as
View SolutionGiven the LPP max Z=2x+3y
Subject to the constraints
3x+y≤3
x≥0,y≥0
show that the corner points of the LPP are (0,0) ,(1,0) and (0,3)
View SolutionFind the graph of linear inequation in xy plane y−3<0
View Solutionlogxry−pz=logypz−rx=lozqx−py show that xpyqzr=1
View SolutionThe feasible region for a LPP is shown in the following figure. Evaluate Z=4x+y at each of the corner points of the region. Find the minimum value of Z, if it exists

View SolutionIn the feasible region for a LPP is ..., then the optimal value of the objective function Z= ax + by may or may not exist.
View SolutionFind the optimal solution of the above LPP and the maximum value of Z
View SolutionIf an LPP admits optimal solution at two consecutive vertices of a feasible region, then
View SolutionThe feasible region for a LPP is shown in the following figure. Evaluate Z=4x+y at each of the corner points of the region. Find the minimum value of Z, if it exists

View SolutionIn the feasible region for a LPP is ..., then the optimal value of the objective function Z= ax + by may or may not exist.
View SolutionDefine Feasible region in LPP.
View SolutionThe feasible region for a LPP is shown in Figure. Find the minimum value of z=11x+7y.
View SolutionThe feasible region for a LPP is shown in Figure. Evaluate z = 4x + y at each of the corner points at this region. Find the minimum value of z, if exists.

View SolutionIf the feasible region for a LPP is …………, then the optimal value of the objective function z = ax + by may or may not exist.
View Solution