The velocity of a particle is zero at t=0
The acceleration at t = 0 must be zero
The acceleration at t=0 may be zero
If the acceleration is zero from t = 0 to t = 10s, the speed is also zero in this interval
If the speed is zero from t = 0 to t = 10s the acceleration is also zero in this interval
The correct Answer is:B, C, D
At t= 0 , acceleration may or may not be zero.
t=0 , speed is zero . So , without acceleration , particle remains at rest .
Similar Questions
Knowledge Check
- Question 1 - Select One
The velocity of a particle is zero at time t = 2s, then
Adisplacement must be zero in the interval t = 0 to t = 2 s.Bacceleration may be zero at t = 2 s.Cvelocity must be zero for t>2s .Dacceleration must be zero at t = 2 s. - Question 2 - Select One
Statement-I : When velocity of a particle is zero then acceleration of particle is zero.
Statement-II : Acceleration is equal to rate of change of velocity.AStatement-I is true, Statement-II is true, Statement-II is correct explanation for Statement-IBStatement-I is true, Statement-II is true, Statement-II is NOT a correct explanation for Statement-ICStatement-I is true, Statement-II is falseDStatement-I is false, Statement-II is true. - Question 3 - Select One
The acceleratin of a particle increases linearly with time t as 6t. If the initial velocity of the particles is zero and the particle starts from the origin, then the distance traveled by the particle in time t will be
AtBt2Ct3Dt4
If the instantaneous velocity of a particle is zero, will its instantaneous acceleration be necessarily zero
View SolutionThe velocity time relation of a particle is given by v =(3t2−2t−1)m/s Calculate the position and acceleration of the particle when velocity of the particle is zero . Given the initial position of the particle is 5m .
View SolutionAcceleration-time graph of a particle moving in a straight line is as shown in figure. At time t=0, velocity of the particle is zero. Find

(a) average acceleration in a time interval from t=6s to t=12s,
(b) velocity of the particle at t=14s.View SolutionThe velocity of a particle varies with time as →v=3ˆi+(4−5t)ˆjms−1. Find the average velocity of the particle for a time interval between t=0 and a time when the speed of the particle becomes minimum.
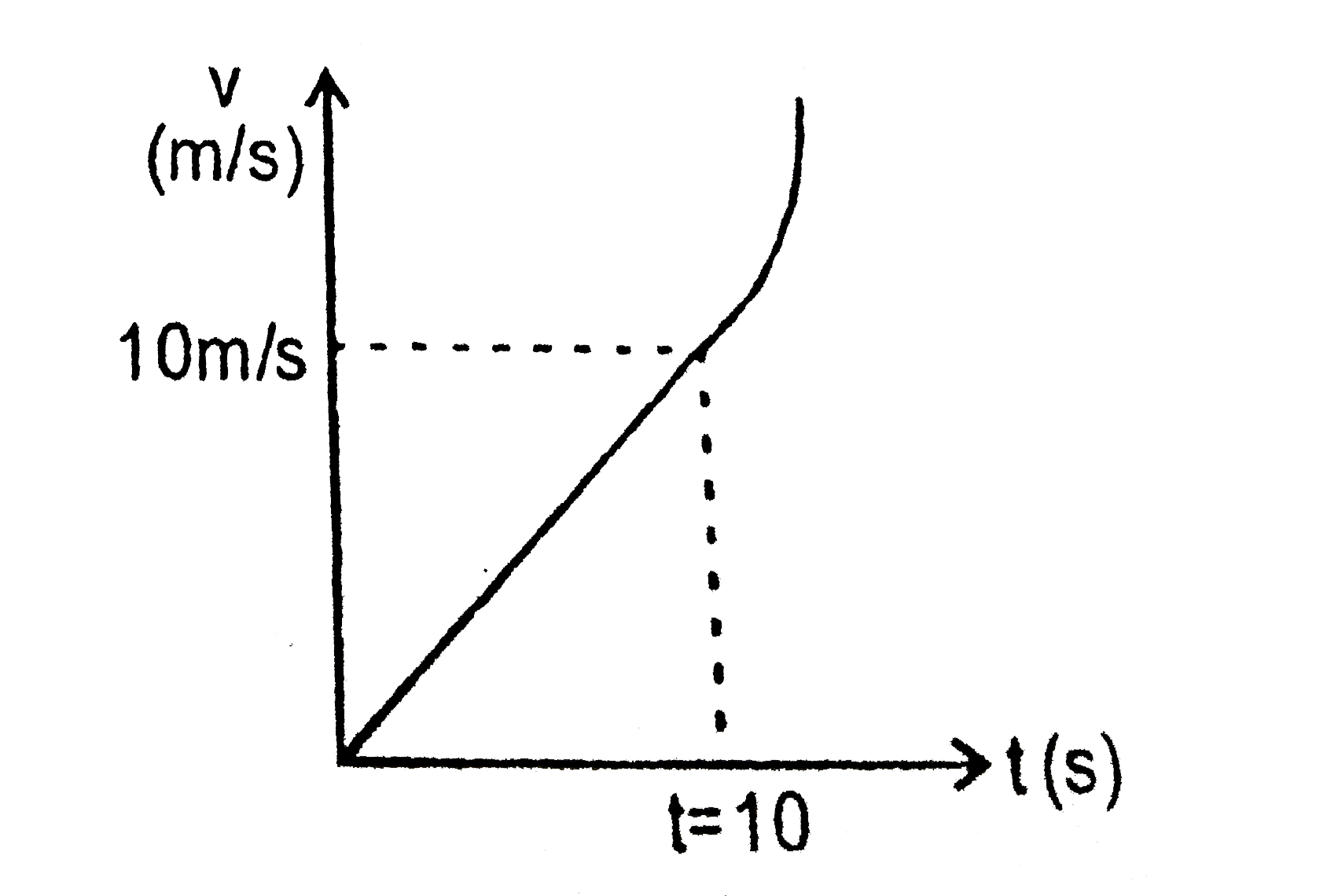
View SolutionA particle is moving in a straight line as :
a=1m/s20≤t≤10
a=2tt>10
where t is the time and a is the acceleration. If initial velocity of the particla is zero then :
 View Solution
View Solution
