A car accelerates from rest at a constant rate for some time after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t, the maximum velocity acquired by the car is given by :
αβα+βt
α+βαβt
α2+β2βα
α+β2βα
The correct Answer is:A
To solve the problem step by step, we will analyze the motion of the car during its acceleration and deceleration phases.
Step 1: Define the Variables
- Let α be the constant acceleration of the car.
- Let β be the constant deceleration of the car.
- Let t1 be the time during which the car accelerates.
- Let t2 be the time during which the car decelerates.
- The total time elapsed is t=t1+t2.
Step 2: Determine the Maximum Velocity
During the acceleration phase, the car starts from rest and accelerates to a maximum velocity vmax. The relationship between acceleration, time, and velocity is given by:
vmax=αt1
Step 3: Determine the Deceleration Phase
During the deceleration phase, the car comes to rest from the maximum velocity vmax. The relationship for deceleration is:
vmax=βt2
Since the car comes to rest, we can express t2 in terms of vmax:
t2=vmaxβ
Step 4: Relate the Times
From the total time equation, we have:
t=t1+t2
Substituting t2 from the deceleration phase:
t=t1+vmaxβ
Step 5: Substitute vmax
Now, substitute vmax=αt1 into the equation:
t=t1+αt1β
Factoring t1 out:
t=t1(1+αβ)
Step 6: Solve for t1
Rearranging gives:
t1=t1+αβ=tββ+α
Step 7: Substitute Back to Find vmax
Now substitute t1 back into the equation for vmax:
vmax=αt1=α(tββ+α)
Thus, we have:
vmax=αβtβ+α
Final Answer
The maximum velocity acquired by the car is given by:
vmax=αβtα+β
- Let α be the constant acceleration of the car.
- Let β be the constant deceleration of the car.
- Let t1 be the time during which the car accelerates.
- Let t2 be the time during which the car decelerates.
- The total time elapsed is t=t1+t2.
During the acceleration phase, the car starts from rest and accelerates to a maximum velocity vmax. The relationship between acceleration, time, and velocity is given by:
vmax=αt1
During the deceleration phase, the car comes to rest from the maximum velocity vmax. The relationship for deceleration is:
vmax=βt2
Since the car comes to rest, we can express t2 in terms of vmax:
t2=vmaxβ
From the total time equation, we have:
t=t1+t2
Substituting t2 from the deceleration phase:
t=t1+vmaxβ
Now, substitute vmax=αt1 into the equation:
t=t1+αt1β
Factoring t1 out:
t=t1(1+αβ)
Rearranging gives:
t1=t1+αβ=tββ+α
Now substitute t1 back into the equation for vmax:
vmax=αt1=α(tββ+α)
Thus, we have:
vmax=αβtβ+α
The maximum velocity acquired by the car is given by:
vmax=αβtα+β
Similar Questions
A car acceleration form rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t evaluate (a) the maximum velocity attained and (b) the total distance travelled.
View SolutionA car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t seconds. Then evalute (a) the maximum velocity reached and (b) the total distance travelled.
View Solution
Knowledge Check
A car accelerates from rest at a constant rate α for sometime , after which it decelerates at a constant rate β and comes to rest. If T is the total time elapsed, the maximum velocity acquired by the car is
A(αβα+β)TB((α+βαβ)TC(α2+β2αβ)TD12αTβA car accelerates from rest at a constant rate for some time after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t, the maximum velocity acquired by the car is given by :
Aab(a+b)tBab(a−b)tCat2(a+b)Dtb2(a+b)A car accelerates from rest at a constant rate of 2ms−2 for some time. The it retatds at a constant rate of 4ms−2 and comes to rest. It remains in motion for 6s.
AIts maximum speed is 8ms−1BIts maximum speed is 6ms−1CIt travelled a total distance of 24mDIt travelled a total distance of 18m
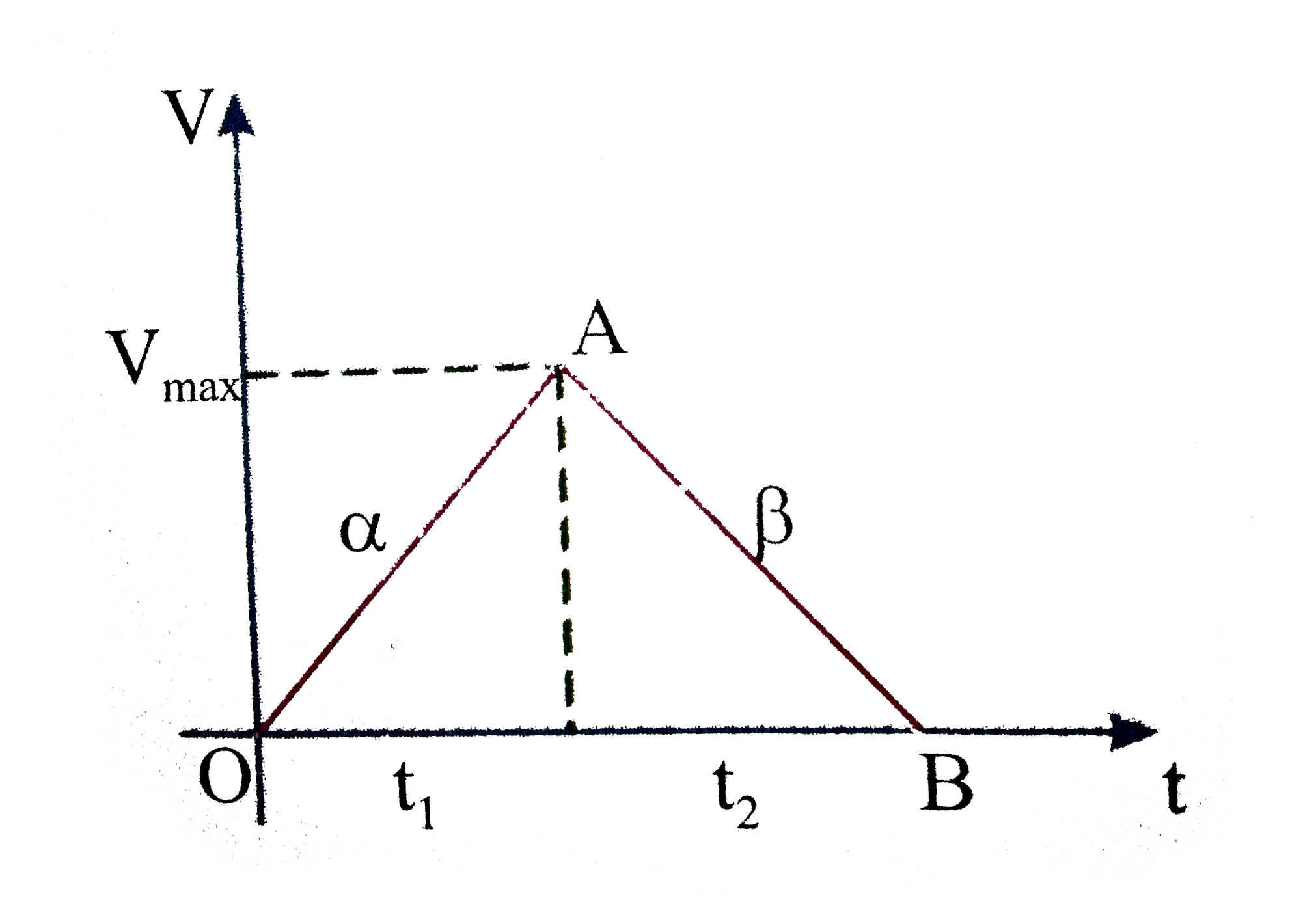
A bus accelerated from rest at a constant rate α for some time, after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t seconds. Then evaluate following parameters from the given graph
(a) the maximum velocity achieved.
(b) the total distance travelled graphically and
(c) Average velocity.
View SolutionA car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β and ultimately comes to rest.If the total time-lapse is t, what is the total distance described and maximum velocity reached ?
View SolutionA particle accelerates from rest at a constant rate for some time and attains a velocity of 8 m/sec. Afterwards it decelerates with the constant rate and comes to rest. If the total time taken is 4 sec, the distance travelled is
View SolutionA car acceleration from rest at a constant rate 2m/s2 for some time. Then, it retards at a constant rate of 4m/s2 and comes to rest. If it remains motion for 3 second, then the maximum speed attained by the car is:-
View SolutionA car accelerates from rest at constant rate of 2ms−2 for some time. Then it retards at a constant rate of 4ms−2 and comes to rest. It remains in motion for 3 seconds
View Solution

