A metallic rod of length 1m is rigidly clamped at its mid point. Longirudinal stationary wave are setup in the rod in such a way that there are two nodes on either side of the midpoint. The amplitude of an antinode is $2 \times 10^{- 6} m$ . Write the equation of motion of a point 2 cm from the midpoint and those of the constituent waves in the rod, (Young,s modulus of the material of the rod $= 2 \times 10^{11} N m^{- 2}$ , density $= 8000 k g - m^{- 3}$ ). Both ends are free.

Video Solution

Text Solution

Verified by Experts

(i) $y = 2 \times 10^{- 6} cos 5 π (0.5 \pm 0.02) sin 25000 π t$ ,
(ii) $y_{1} = 10^{- 6} sin (25000 π t - 5 π x), y_{2} = 10^{- 6} sin (25000 π t + 5 π x)$
$y, y_{1}, y_{2}$ & x are in m & t is in sec
As found in case of strings, in case of rods also the clamped point behave as a node while the free end antinode. The situation is shown in the figure

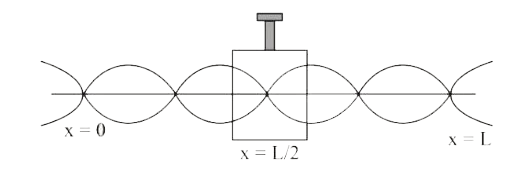
Because the distance between two consecutive nodes is $(λ / 2)$ while between a node and antinode is $λ / 4$ , hence
$4 \times [\frac{λ}{2}] + 2 [\frac{λ}{4}] = L or λ = \frac{2 \times 1}{5} = 0.4 m$
Further, it is given that $Y = 2 \times 10^{11} N / m^{2} and ρ = 8 \times 10^{3} k g / m^{3}$
$v = \sqrt{\frac{Y}{ρ}} = \sqrt{\frac{2 \times 10^{11}}{8 \times 10^{3}}} = 5000 m / s$
Hence, from $v = n λ, n = \frac{v}{λ} = \frac{5000}{0 A} = 12500 H z$
Now if incident and reflected waves along the rod are $y_{1} = A sin (ω t - k x) and y_{2} = A sin (ω t + k x + ϕ)$
The resultant will be $y = y_{1} + y_{2} = A [sin (ω t - k x) + sin (ω t + k x + ϕ)] = 2 A cos (k x + \frac{ϕ}{2}) sin (ω t + \frac{ϕ}{2})$
Because there is an antinode at the free end of the rod, hence amplitude is maximum at x=0, So
$cos (k \times 0 + \frac{ϕ}{2}) = maximum = 1$ i.e., $ϕ = 0$
And $A_{max} = 2 A = 2 \times 10^{- 6} m (g i v e n)$
$y = 2 \times 10^{- 6} cos [\frac{2 π x}{λ}] sin (2 π n t)$
Putting values of $λ and n$ , we get $y = 2 \times 10^{- 6} cos 5 π x sin 25000 π t$
Now, because for a point 2 cm from the midpoint x=(0.50 $\pm 0.02$ )
Hence $y = 2 \times 10^{- 6} cos 5 π (0.5 \pm 0.02) sin 25000 π t$ .

Updated on:21/07/2023

Class 12 PHYSICS WAVE OPTICS

Knowledge Check

If the young's modulus of the material of the rod is $2 \times 10^{11} N / m^{2}$ and its density is $8000 k g / m^{3}$ then the time taken by a sound wave to traverse 1m of the rod will be
A $10^{- 4} s$
B $2 \times 10^{- 4} s$
C $10^{- 2} s$
D $2 \times 10^{- 2} s$
A metallic rod of length $1 m$ has one end free and other end rigidly clamped. Longitudinal stationary waves are set up in the rod in such a way that there are total six antinodes present along the rod. The amplitude of an antinode is $4 \times 10^{- 6} m$ . young's modulus and density of the rod are $6.4 \times 10^{10} N / m^{2}$ and $4 \times 10^{3} K g / m^{3}$ respectively. Consider the free end to be at origin and at $t = 0$ particles at free end are at positive extreme.
The magnitude of strain at midpoint of the rod at $t = 1 sec$ is
A $11 \sqrt{3} π \times 10^{- 6}$
B $11 \sqrt{2} π \times 10^{- 6}$
C $10 \sqrt{3} π \times 10^{- 6}$
D $10 \sqrt{2} π \times 10^{- 6}$
A metallic rod of length $1 m$ has one end free and other end rigidly clamped. Longitudinal stationary waves are set up in the rod in such a way that there are total six antinodes present along the rod. The amplitude of an antinode is $4 \times 10^{- 6} m$ . young's modulus and density of the rod are $6.4 \times 10^{10} N / m^{2}$ and $4 \times 10^{3} K g / m^{3}$ respectively. Consider the free end to be at origin and at $t = 0$ particles at free end are at positive extreme.
The equation describing stress developed in the rod is
A $140.8 π \times 10^{4} cos (\frac{11}{2} π x + π) cos (22 π \times 10^{3} t)$
B $140.8 π \times 10^{4} sin (\frac{11}{2} π x + π) cos (22 π \times 10^{3} t)$
C $128 π \times 10^{4} cos (5 π x + π) cos (20 π \times 10^{3} t)$
D $128 π \times 10^{4} sin (5 π x + π) cos (20 π \times 10^{3} t)$

Similar Questions

Knowledge Check

If the young's modulus of the material of the rod is $2 \times 10^{11} N / m^{2}$ and its density is $8000 k g / m^{3}$ then the time taken by a sound wave to traverse 1m of the rod will be

Recommended Questions

Similar Questions

Knowledge Check

If the young's modulus of the material of the rod is 2×1011N/m2 and its density is 8000kg/m3 then the time taken by a sound wave to traverse 1m of the rod will be

Recommended Questions

If the young's modulus of the material of the rod is $2 \times 10^{11} N / m^{2}$ and its density is $8000 k g / m^{3}$ then the time taken by a sound wave to traverse 1m of the rod will be