A 10 m long horizontal stainless steel wire AB of mass 1 kg whose end A is fixed, is connected to a massless string BC passing over a smooth pulley. String BC is connected to a container of mass 2 kg at end C. Water (density =1×103kg/m3) is poured int he container at a constant rate of 2.25 litre/sec at t=0. also t=0, a puls is generated at end A.
Time taken by the pulse to reach point B is 0.612 sec
Time taken by the pulse to reach point B is 0.212 sec
Tension in the string at this moment is 33.77 N
Tension in the string at this moment is 24.77 N
The correct Answer is:A, B
To solve the problem step by step, we will follow the logical flow of the video transcript while providing clear explanations and calculations.
Step 1: Understanding the System
We have a stainless steel wire AB of length 10 m and mass 1 kg, with one end fixed at point A. The other end is connected to a massless string BC that goes over a smooth pulley and is attached to a container of mass 2 kg. Water is poured into the container at a rate of 2.25 liters per second.
Step 2: Finding the Mass per Unit Length (μ) of the Wire
The mass per unit length (μ) of the wire can be calculated as follows:
μ=mass of wirelength of wire=1kg10m=0.1kg/m
Step 3: Finding the Rate of Mass Increase in the Container
The rate at which water is being poured into the container is given as 2.25 liters per second. We convert this to cubic meters:
2.25liters/sec=2.25×10−3m3/sec
The mass of water added per second can be calculated using the density of water (1000 kg/m³):
mass rate=density×volume rate=1000kg/m3×2.25×10−3m3/sec=2.25kg/sec
Step 4: Expression for Tension (T) in the String
At any time t, the total mass in the container is the sum of the mass of the container and the mass of the water:
Total mass=2kg+2.25kg/sec×t
The tension in the string due to the weight of this mass is:
T(t)=g×Total mass=10m/s2×(2+2.25t)=20+22.5tN
Step 5: Finding the Velocity (v) of the Wave in the Wire
The velocity of the wave in the wire is given by the formula:
v=√Tμ
Substituting the expression for tension:
v(t)=√20+22.5t0.1=√200+225t
Step 6: Time Taken for the Wave to Travel 10 m
We need to find the time T taken for the wave to travel from A to B (10 m). We can express the velocity as:
dxdt=√200+225t
Integrating both sides, we have:
∫100dx=∫T0√200+225tdt
The left side integrates to 10, and the right side can be solved using substitution.
Step 7: Solving the Integral
Let u=200+225t, then du=225dt or dt=du225.
When t=0, u=200, and when t=T, u=200+225T.
The integral becomes:
10=∫200+225T200√udu225
Calculating this integral gives:
10=1225⋅23(u3/2)200+225T200
Solving for T will yield the time taken for the wave to reach point B.
Step 8: Finding the Tension at Time T
Once we have T, we can substitute it back into the tension equation:
T=20+22.5T
This will give us the tension in the string when the wave reaches point B.
Final Results
After performing the calculations, we find:
- The time taken for the wave to reach point B is approximately 0.612seconds.
- The tension in the string at that time is approximately 33.77N.
We have a stainless steel wire AB of length 10 m and mass 1 kg, with one end fixed at point A. The other end is connected to a massless string BC that goes over a smooth pulley and is attached to a container of mass 2 kg. Water is poured into the container at a rate of 2.25 liters per second.
The mass per unit length (μ) of the wire can be calculated as follows:
μ=mass of wirelength of wire=1kg10m=0.1kg/m
The rate at which water is being poured into the container is given as 2.25 liters per second. We convert this to cubic meters:
2.25liters/sec=2.25×10−3m3/sec
The mass of water added per second can be calculated using the density of water (1000 kg/m³):
mass rate=density×volume rate=1000kg/m3×2.25×10−3m3/sec=2.25kg/sec
At any time t, the total mass in the container is the sum of the mass of the container and the mass of the water:
Total mass=2kg+2.25kg/sec×t
The tension in the string due to the weight of this mass is:
T(t)=g×Total mass=10m/s2×(2+2.25t)=20+22.5tN
The velocity of the wave in the wire is given by the formula:
v=√Tμ
Substituting the expression for tension:
v(t)=√20+22.5t0.1=√200+225t
We need to find the time T taken for the wave to travel from A to B (10 m). We can express the velocity as:
dxdt=√200+225t
Integrating both sides, we have:
∫100dx=∫T0√200+225tdt
The left side integrates to 10, and the right side can be solved using substitution.
Let u=200+225t, then du=225dt or dt=du225.
When t=0, u=200, and when t=T, u=200+225T.
The integral becomes:
10=∫200+225T200√udu225
Calculating this integral gives:
10=1225⋅23(u3/2)200+225T200
Solving for T will yield the time taken for the wave to reach point B.
Once we have T, we can substitute it back into the tension equation:
T=20+22.5T
This will give us the tension in the string when the wave reaches point B.
After performing the calculations, we find:
- The time taken for the wave to reach point B is approximately 0.612seconds.
- The tension in the string at that time is approximately 33.77N.
Similar Questions
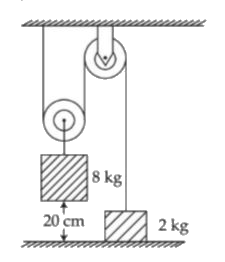
The boxes of masses 2 kg and 8 kg are connected by a massless string passing over smooth pulleys. Calculate the time taken by box of mass 8 kg to strike the ground starting from rest. (use g=10 m/s2):
View SolutionTwo bodies of masses 11kg and 11.5kg are connected by a long light string passing over a smooth pulley Calculate velocity and height ascended/descended by each body at the end of 4s .
View Solution
Knowledge Check
Two bodies of mass 3 kg and 4 kg are suspended at the ends of massless string passing over a frictionless pulley. The acceleration of the system is (g=9.8m/s2)
A4.9m/s2B2.45m/s2C1.4m/s2D9.5m/s2Two bodies of mass 3kg and 4kg are suspended at the ends of massless string passing over a frictionless pulley. The acceleration of the system is (g=9.8m/s2)
A4.9m/s2B2.45m/s2C1.4m/s2D9.5m/s2Two masses of 10 kg and 6 kg connected at the two ends of an inextensible string pass over a smooth frictionless pulley . Calculate acceleration of the system and tension in the string .
A71.5 NB72.5 NC73.5 ND74.5 N
Two masses m1 and m2 are connected to the ends of a massless string that passes over a pulley fixed at the top of a double incline as shown. Assuming m1>m2 acceleration of the system is:

View SolutionTwo masses m1 and m2 are attached to a string which passes over a frictionless smooth pulley. When m1=10kg,m2=6kg, the acceleration of masses is
View SolutionTwo masses 6 kg and 4 kg are connected by massless flexible and inextensible string passing over massless and frictionless pulley.The acceleration of centre of mass is (g=10ms^2)
View SolutionTwo masses 2 kg and 3 kg are attached to the end of the string passed over a pulley fixed at the top. The tension and acceleration are
View SolutionTwo masses m1andm2 are connected to the end of a string passing over a smooth pulley . The magnitude of tension in the string is T and the masses are moving with magnitude of acceleration a . If the masses are interchanged , then
View Solution