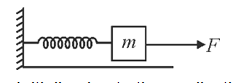
A block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

A

$\frac{F}{\sqrt{m k}}$

B

$π \frac{F}{\sqrt{m k}}$

C

$\frac{F}{π} \sqrt{m k}$

D

$2 π \frac{F}{\sqrt{m k}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Initially, due to the application of constant force, the block starts accelerating due to the right & spring force starts increasing and the speed of the block starts increasing till the spring force becomes equal to constant force ‘F’. So speed is maximum when F=kx $\Rightarrow x = \frac{F}{k}$ .....(i)
using $W = Δ k E$
$w_{s} + W_{F} = \frac{1}{2} m v^{2} \Rightarrow - \frac{1}{2} k x^{2} + F x = \frac{1}{2} m v^{2}$ ...(ii)
So when $x = \frac{F}{k}, v = v_{max}$ .
so from (i)&(ii) $\Rightarrow - \frac{1}{2} k (\frac{F^{2}}{k^{2}}) + F (\frac{F}{K}) = \frac{1}{2} m v_{max}^{2} \Rightarrow \frac{F^{2}}{2} k = \frac{1}{2} m v_{max}^{2} \Rightarrow$ $V_{max} = \frac{F}{\sqrt{m k}}$

Updated on:21/07/2023

|

Class 12 PHYSICS SIMPLE HARMONIC MOTION

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile