A rod of mass 'M' and length '2L' is suspended at its middle by a wire. It exhibits torsional oscillations, if two masses each of 'm' are attached at distance'L/2' from its centre on both sides, it reduces the oscillation frequency by 20%. The value of ratio m/M is close to :
0.57
0.37
0.77
0.17
The correct Answer is:B
τCθ⇒I(d2θ)dt2+Cθ=
Where C is tensional constant
ω1=√CI1
ω2=√CI2
ω2=80100ω1
⇒ω22=0.64ω21 ⇒I=0.64I2
M(2L)212=64100×[M4L212+3mL24×3×2]
4M=64100(4M+6M)⇒mM=38≡0.37
Similar Questions
A disc of mass 'm' is suspended at a point R/2 above its centre. Find its period of oscillation.
View SolutionA uniform disc of mass m and radius r is suspended through a wire attached to its centre. If the time period of the torsional oscillations be T, what is the torsional constant of the wire?
View Solution
Knowledge Check
A uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is
 A2π√lgB2π√2lgC2π√2l3gD2π√l3g
A2π√lgB2π√2lgC2π√2l3gD2π√l3gTwo point masses m and M are separated bya distance L . The distance of the centre of mass of the system from m is
AL(m/M)BL(M/m)CL(Mm+M)DL(mm+M)Two point masses m and M are separated by a distance L . The distance of the centre of mass of the system from m is
AL(m/M)BL(M/m)CL(Mm+M)DL(mm+M)
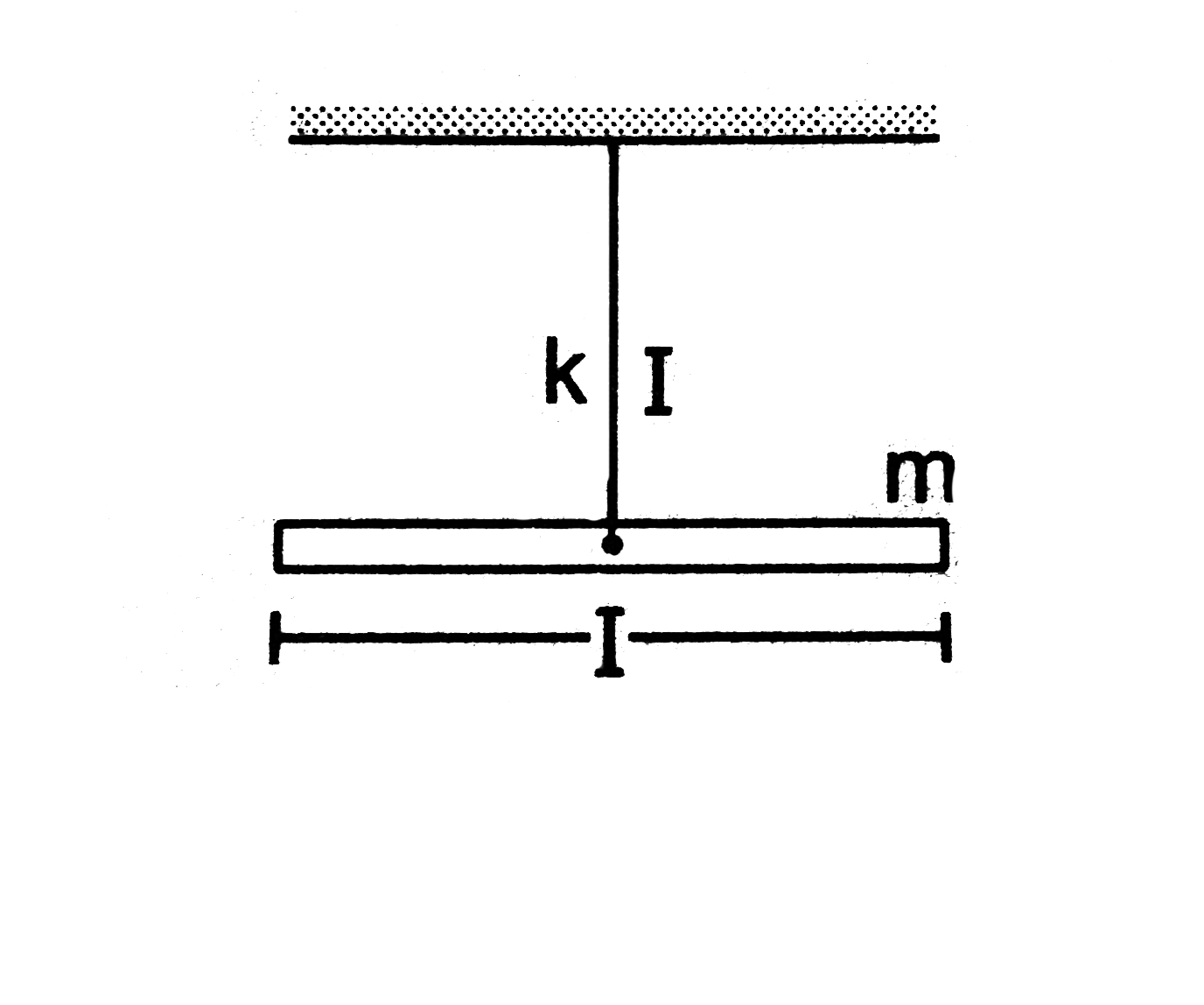
A uniform rod of mass m and length l is suspended through a light wire of length l and torsional constant k as shown in figure. Find the time perid iof the system makes a. small oscillations in the vertical plane about the suspension point and b. angular oscillations in the horizontal plane about the centre of the rod.
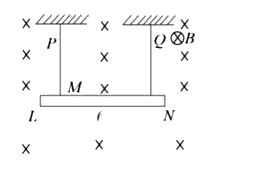
View SolutionA rod of mass M and length l is suspended by two wires P and Q. A uniform magnetic field 'B' is directed into the page. When current through the rod is l. Then the tension in each supporting wire is-
View SolutionA thin rod of length 1 m is suspended from its end and is made to oscillate in a vertical plane. The distance between the point of suspension and centre of oscillation will be :
View SolutionA mass m is suspended from a spring. Its frequency of oscillation is f. The spring is cut into two halves and the same mass is suspended from one of the pieces of the spring. The frequency of oscillation of the mass will be
View SolutionA thin rod of mass m and length l is suspended from one of its ends. It is set into oscillation about a horizontal axis. Its angular speed is ω while passing through its mean position. How high will its centre of mass rise from its lowest position ?
View Solution
