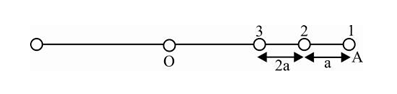
A particle moves with simple harmonic motion in a straight line. In first τs, after starting form rest it travels a destance a, and in next τs it travels 2a, in same direction, then:
amplitude of motion is 4a
time period of oscillations is 6π
time period of oscillations is 6π
time period of oscillations
The correct Answer is:B
As the particle starts from rest so we choose
x(t)=Acosωt
At t=0,x=A
When t=τ,x=A−a
when t=2τ,x=A−3a∴A−a=Acosωt
and A−3a=Acos2ωτ=A(2cos2ωt−1)
⇒(A−3a)=A[2(A−aA)2−1]⇒A−3aA=2(A−aA)2−1
on solving ,A=2a
Now A−a=Acosωτ, ⇒cosωτ=−12=cosπ3⇒ωτ=π3⇒
Similar Questions
A particle moves simple harmonically in a straight line starting from rest. In first 't' sec it travels a distance 'a' and in next 't'sec it travels '2a' in same direction. Then its time period is ?
View SolutionA particle moves with SHM in a straight liine. In the first second afer starting from rest, it travels a distance x1 cm and in the next second it travels a distance x2 cm in the same direction. Prove that the amplitude of oscillation is 2x21/(3x1−x2).
View Solution
Knowledge Check
A particle performs SHM in a straight line. In the first second, starting from rest, it travels a distance a and in the next second it travels a distance b in the same direction. The amplitude of the SHM is
A2a23b−aB3a23a−bC2a23a−bD3a23b−aA particle performs SHM in a straight line. In the first second, starting from rest, it travels a distance a and in the next second it travels a distance b in the same direction. The amplitude of the SHM is
Aa-bB2a−b3C2a23a−bDNone of theseA particle starting from rest travels a distance x in first 2 seconds and a distance y in next two seconds, then
Ay=xBy=2xCy=3xDy=4x
A particle executes SHM in a straight line. In the first second starting from rest it travels distance a and in the next second it travels distance a and in the next second it travels distance d in the same direction. The amplitude of SHM is :
View SolutionA particle moves with simple harmonic motion in a straight line. When the distances of the particle from the equilibrium position are x1 and x2, the corresponding velocities are u1 and u2. Find the period of the moton.
View SolutionA particle experiences constant acceleration for 20 s after starting from rest. If it travels a distance S1 in the first 10 s and distance S2 in the next 10 s, the relation between S1andS2 is :
View SolutionA particle experiences constant acceleration for 20 s after starting from rest. If it travels a distance X1, in the first 10 s and distance X2, in the remaining 10s, then which of the following is true?
View SolutionA particle executes simple harmonic motion along a straight line with an amplitude A . The potential energy is maximum when the displacement is
View Solution
