A particle is placed at the lowest point of a smooth wire frame in the shape of a parabola, lying in the vertical xy-plane having equatioin x2=5y(x,y are in meter). After slight displacement, the particle is set free. Find angular frequency of osciallation (in rad/sec) (Take g=10 m/s2)
The correct Answer is:2
Energy
E=12mv2+mgy=12mv2+mg(x25)
For dEdt=0,a=−(g2.5)x
SO ω=(g2.5)1/2=(102.5)1/2=1rad/sec
Similar Questions
A particle of mass 5×10−5kg is placed at the lowest point of a smooth parabola having the equation 20t2=y (x, y in m). Here y is the vertical height. If it is displaced slightly and it.is constrained to move along the parabola, find the angular frequency (in rad/s) of small oscillations.
View SolutionA particle of mass 1 mg and charge q is lying at the mid-point of two stationary particles kept at a distance '2 m' when each is carrying same charge 'q'. If the free charged particle is displaced from its equilibrium position through distance 'x' (x<<1 m). The particle executes SHM. Its angular frequency of oscillation will be __________ ×105 rad/s if q2=10C2
View Solution
Knowledge Check
A smooth wire frasme is in the shape of a parabola y=5x2 . It is being rotated about y-axis with an angular velocity ω. A small bead of mass (m=1kg) is at point P and is in equilibrium with respect to the frame. Then the angular velocity ω is (g=10m/s2)
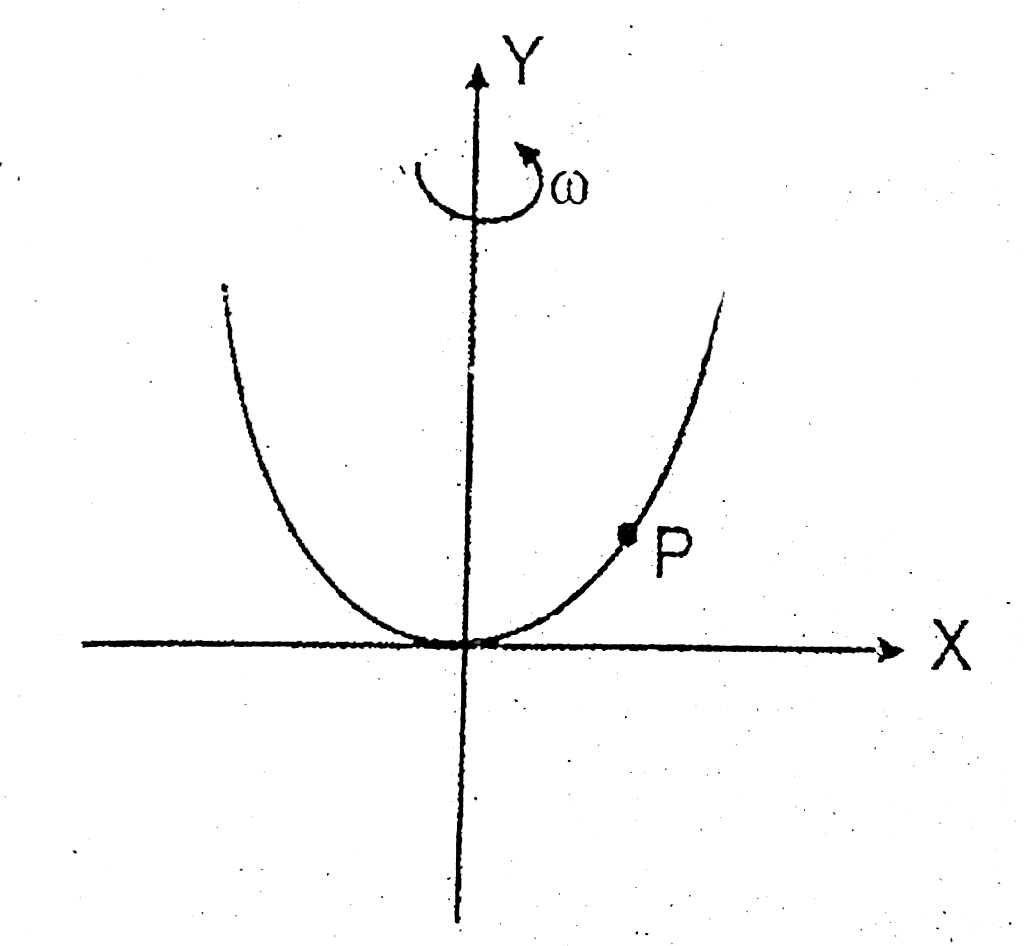 Aω=5rad/secBω=10rad/secCω=20rad/secDDepends of x-coordinate of particle
Aω=5rad/secBω=10rad/secCω=20rad/secDDepends of x-coordinate of particleThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]
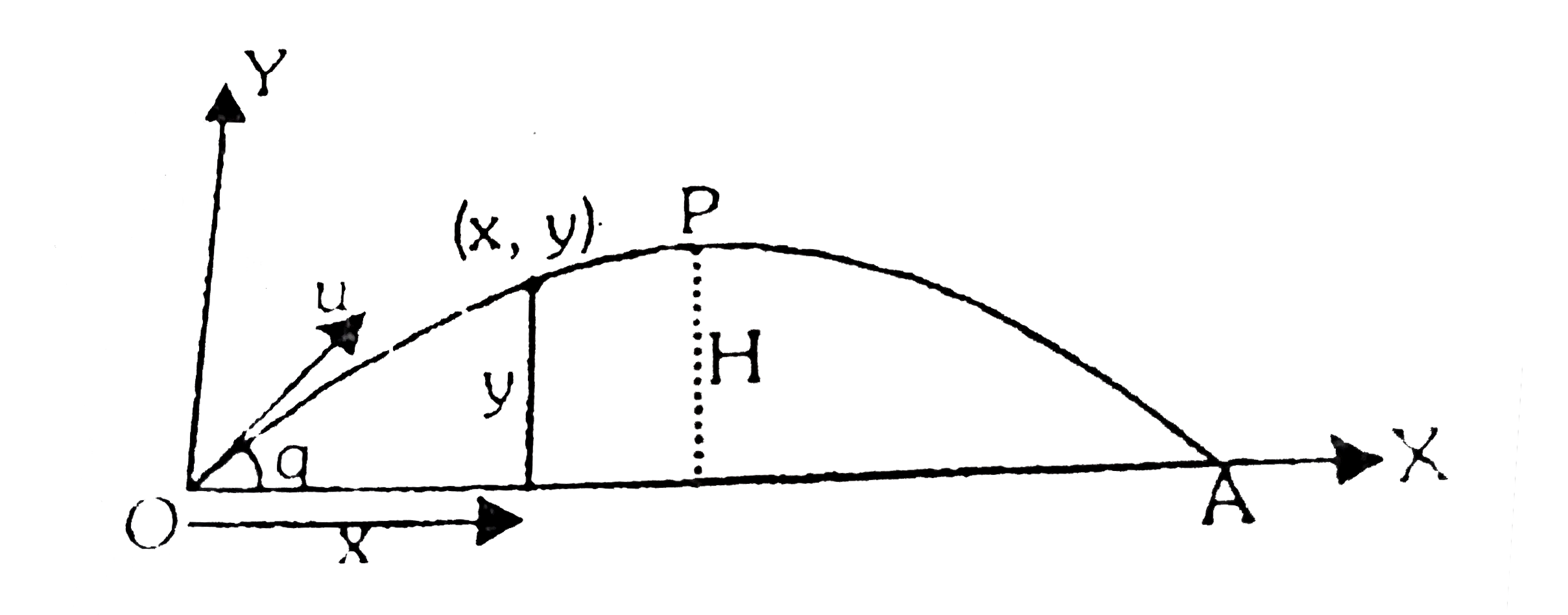
Range OA is :-A√32B√34C√3D38Angular velocity of smooth parabolic wire y = 4c(x^2) about axis of parabola in vertical plane if bead of mass m does not slip at (a,b) will be
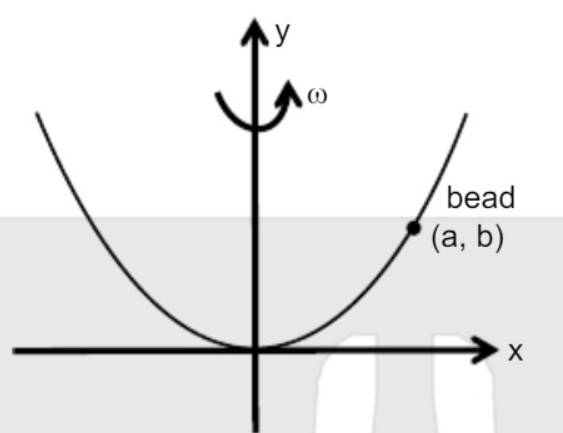 A√2gcB2√2gcbC2√2gcabD2√2gc
A√2gcB2√2gcbC2√2gcabD2√2gc
A particle having mass 2 kg is moving along straight line 3x+4y=5 with speed 8m/s . Find angular momentum of the particle about origin, x and y are in meters.
View SolutionFrequency of a particle executing SHM is 10Hz. The particle is suspended form a vertical spring. At the highest point of its oscillation the spring is unstretched. Find the maximum speed of the particle: (g=10m/s2)
View SolutionA particle mass 1 kg is moving along a straight line y=x+4. Both x and y are in metres. Velocity of the particle is 2m/s. Find the magnitude of angular momentum of the particle about origin.
View SolutionThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]

Maximum height H is :-
View SolutionThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]

Angle of projection θ is :-
View Solution