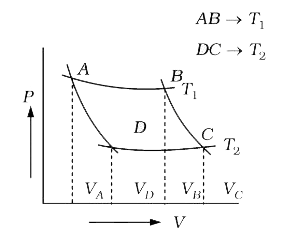
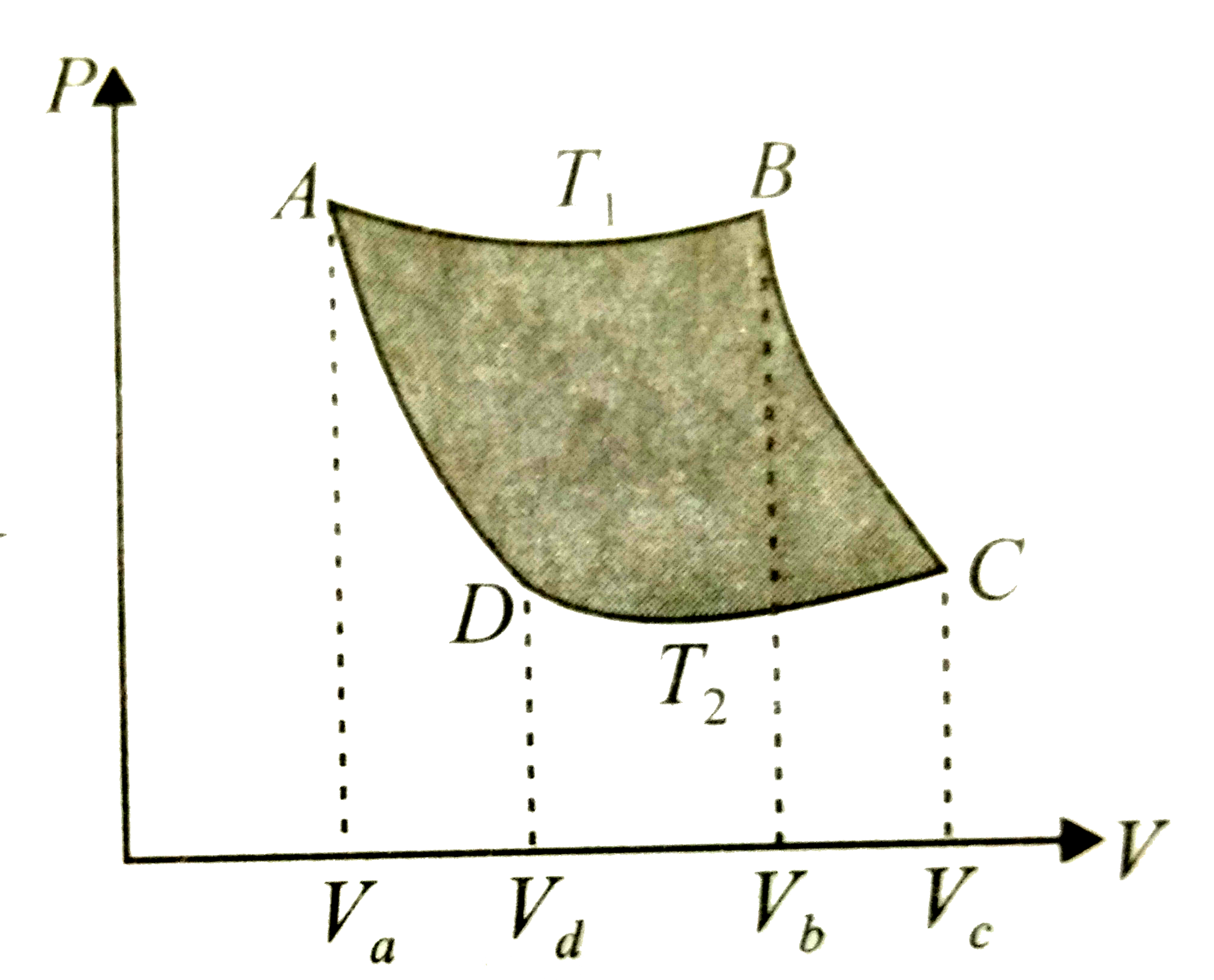
In the following P–V diagram of an ideal gas, two adiabates cut two isotherms at T1 and T2 The value of VB/VC is :
=VA/VD
<VA/VD
>VA/VD
cannot say
The correct Answer is:A
BC is adiabatic process
T1Vγ−1B=T2Vγ−1C
T1T2=[VCVB]γ−1 ..(i)
Da is adiabatic process T2Vγ−1D=T1Vγ−1A
T1T2=(VDVA)γ−1 ...(ii)
By Equation (i) and (ii)
VC=VB=VDVA VBVC=VAVD
Similar Questions
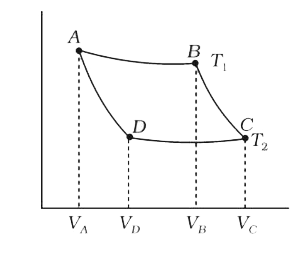
Two different adiabatic curves for the same gas intersect two isothermals at T1,andT2 as shown in P−V diagram, (figure). How does the ratio (Va/Vd) compare with the ratio (Vb/Vc) ?
View SolutionThe temperature of an ideal gas undergoing adiabatic expansion varies with volume as T∝V−34, then the value of CPCV for the gas is
View Solution
Knowledge Check
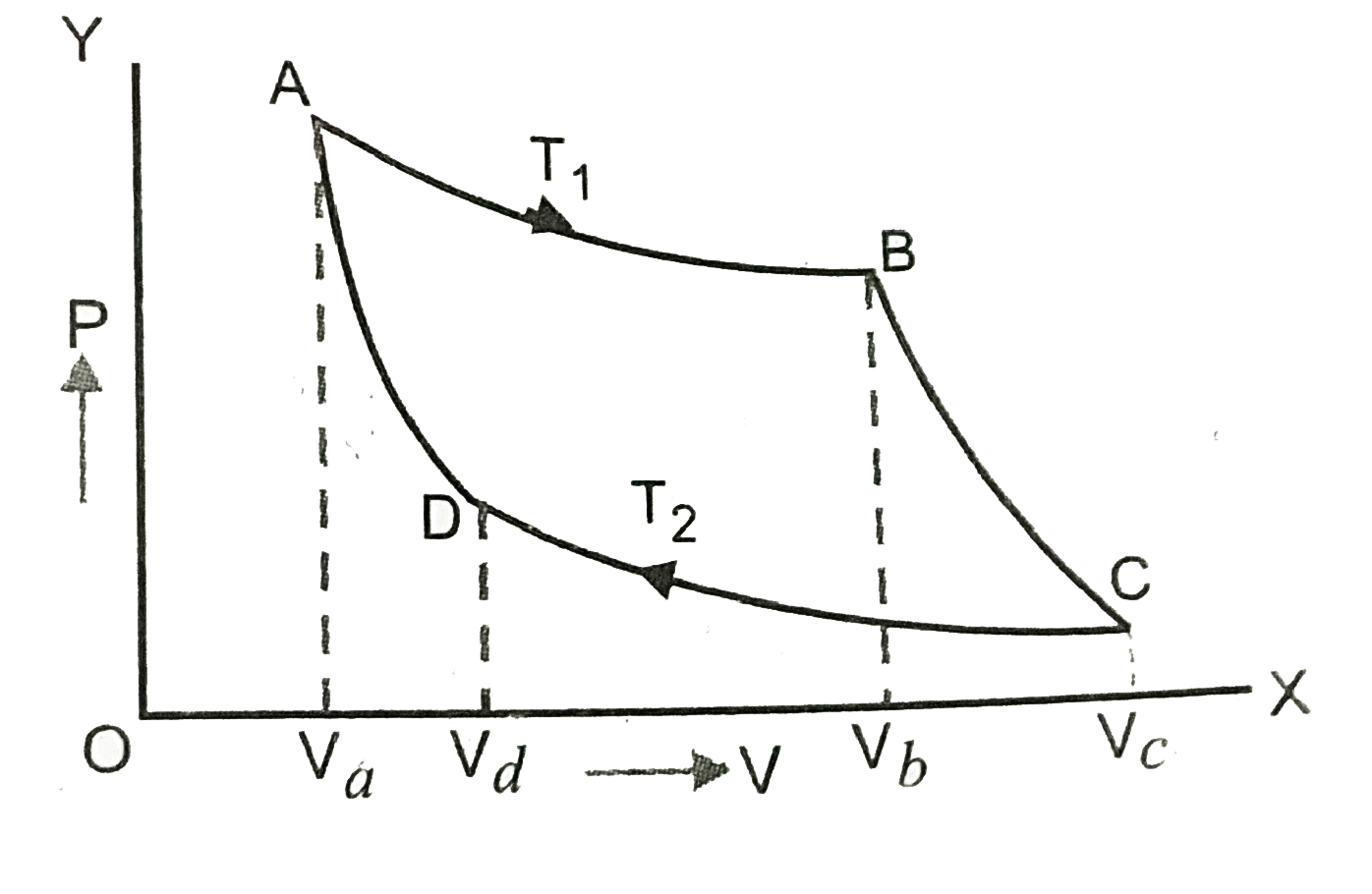
In the following P-V diagram of an ideal gas, two adiabates cut two isotherms at T1=300KandT2=200K. The value of VA=2 unit, VB=8 unit, VC=16 unit. Find the value of VD .
 A4 unitB<4 unitC>5 unitD5 unit
A4 unitB<4 unitC>5 unitD5 unitIn the following P-V diagram two adiabatics cut two isothermals at temperature T1andT2 (fig). The value of VaVd will be
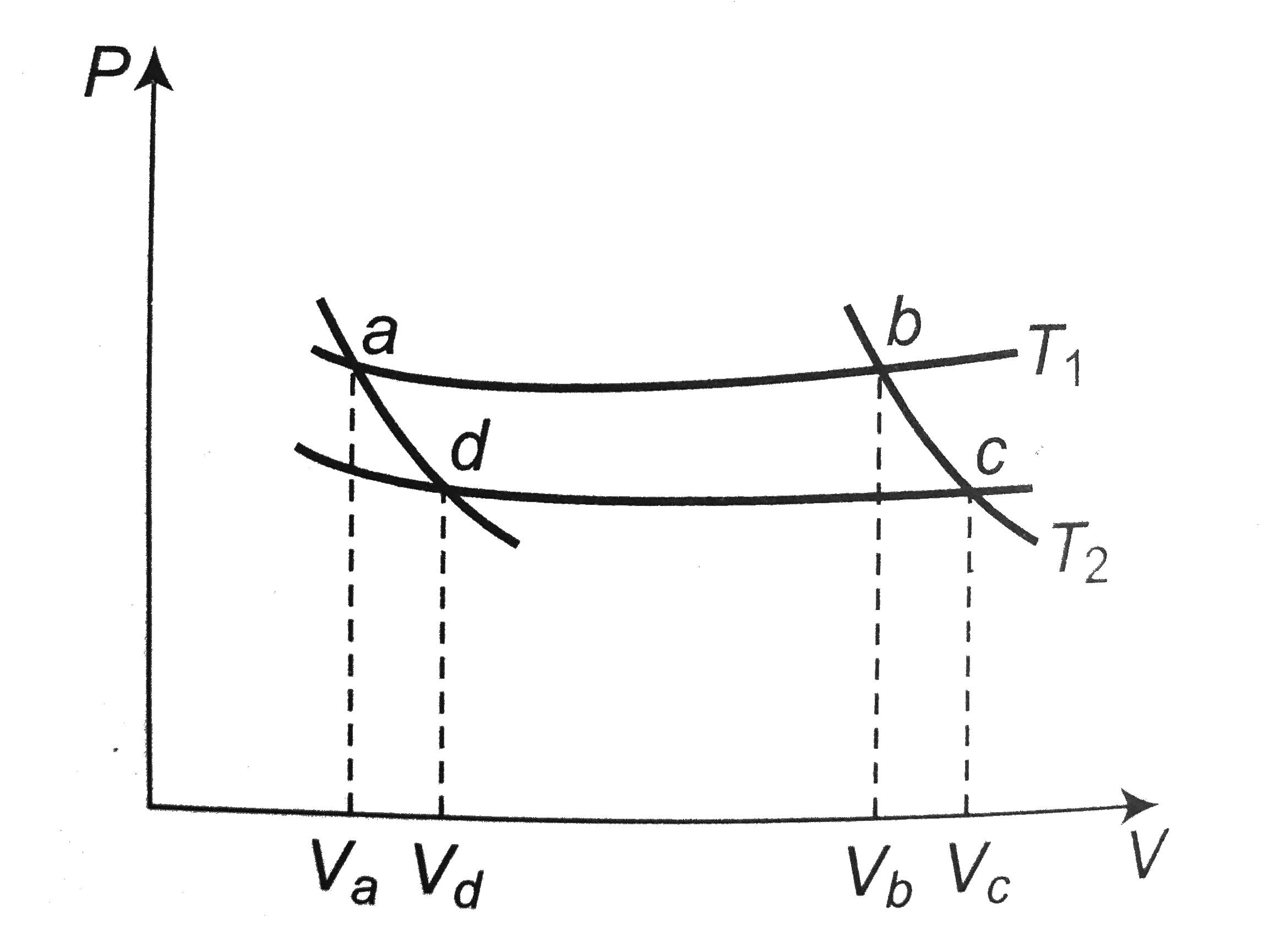 AVbVcBVcVbCVdVaDVbVc
AVbVcBVcVbCVdVaDVbVcAn ideal gas expanded adiabaticlly such that , T ∝V−1/2 then :
Aγ of gas will be 1.5BV∝P2/3CP∝T3DP∝T2
The p−V diagrams of same mass of a gas are drawn at two different temperatues T1 and T2 Explain whether T1>T2> or T2>T1.
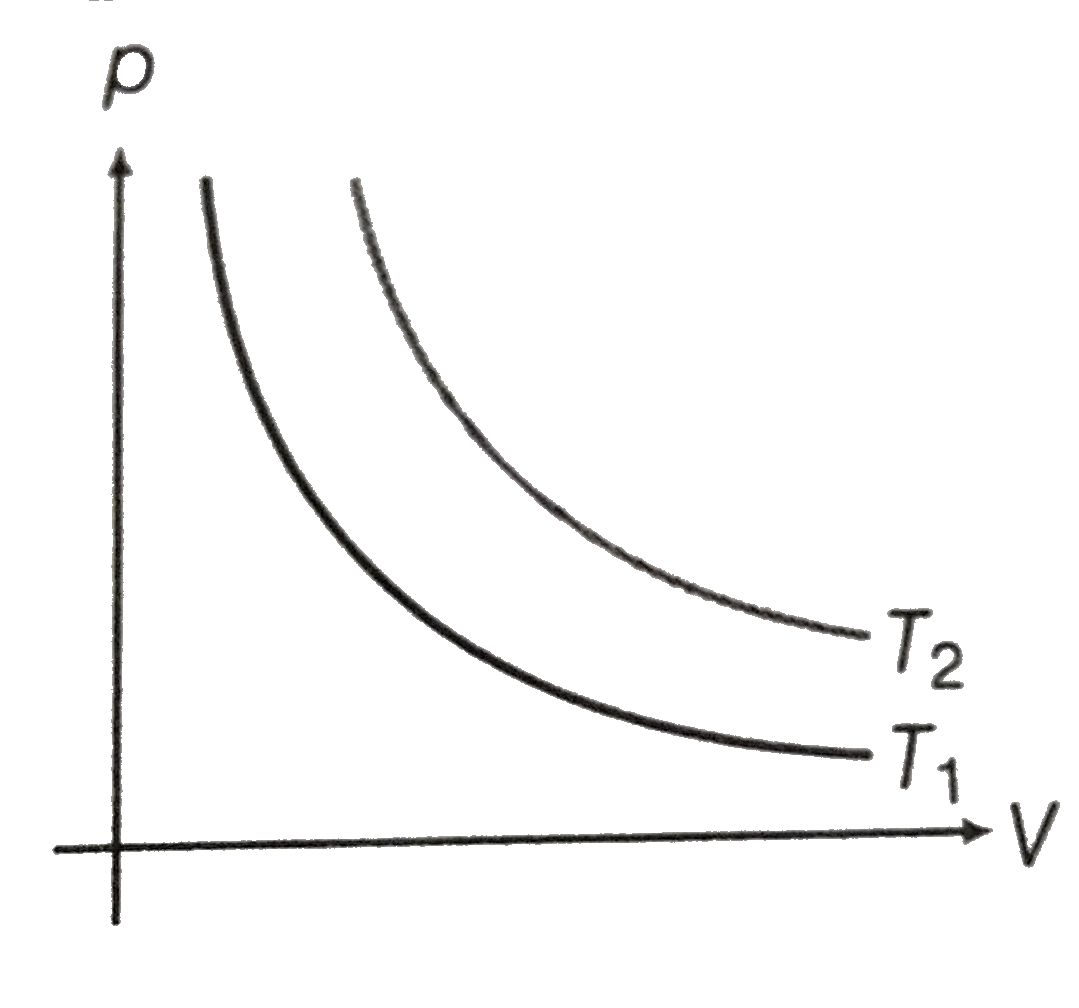
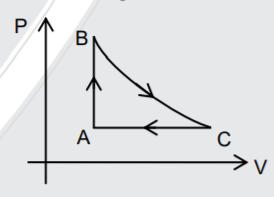
View SolutionFor the given P-V graph for an ideal gas, chose the correct V-T graph. Process BC is adiabatic.
View SolutionTwo different adiabatic parts for the same gas intersect two isothermals at T1andT2 shown in P-V diagram . Then the ratio of VaVb will be
View SolutionThe temperature of an ideal gas undergoing adiabatic expansion varies with volume as T∝V−34, then the value of CPCV for the gas is
View SolutionAn ideal gas in thermally insulated vessel at internal (pressure)=P1,(volume)=V1 and absolute temperature=T1 expands irreversiby against zero external, pressure , as shown in the diagram,
The final internal pressure, volume and absolute temperature of the gas are p2,V2andT2, respectively . For this expansion

View Solution

