A planet of mass M, has two natural satellites with masses m1 and m2. The radii of their circular orbits are R1 and R2 respectively. Ignore the gravitational force between the satellites. Define v1,L1,K1 and T1 to be, respectively, the orbital speed, angular momentum, kinetic energy and time period of revolution of satellite 1 , and v2,L2,K2 and T2 to be he corresponding quantities of satellite 2. Given m1/m2=2 and R1/R2=1/4, match the ratios in List-I to the numbers in List-II.
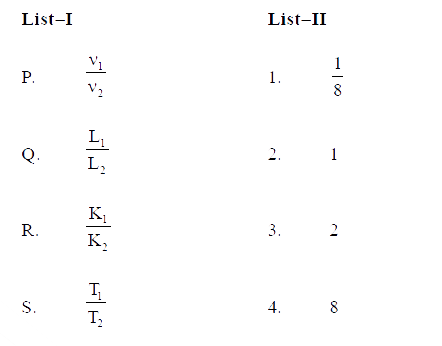
A-S, B-Q, C-P, D-R
A-R, B-Q, C-R, D-P
A-Q, B-R, C-P, D-S
A-Q, B-R, C-S, D-P
The correct Answer is:B
v∝1√r , Hence correct answer is ‘B’ Also , T∝r3/2 , K∝mr
Similar Questions
A planet of mass , has two natural satellites with masses and . The radii of their circular orbits are and respectively. Ignore the gravitational force between the satellites. Define , and to be, respectively, the orbital speed, angular momentum, kinetic energy and time period of revolution of satellite 1, and , , and to be the corresponding quantities of satellite 2. Given/2and/1/4, match the ratios in List-I to the numbers in List-II.
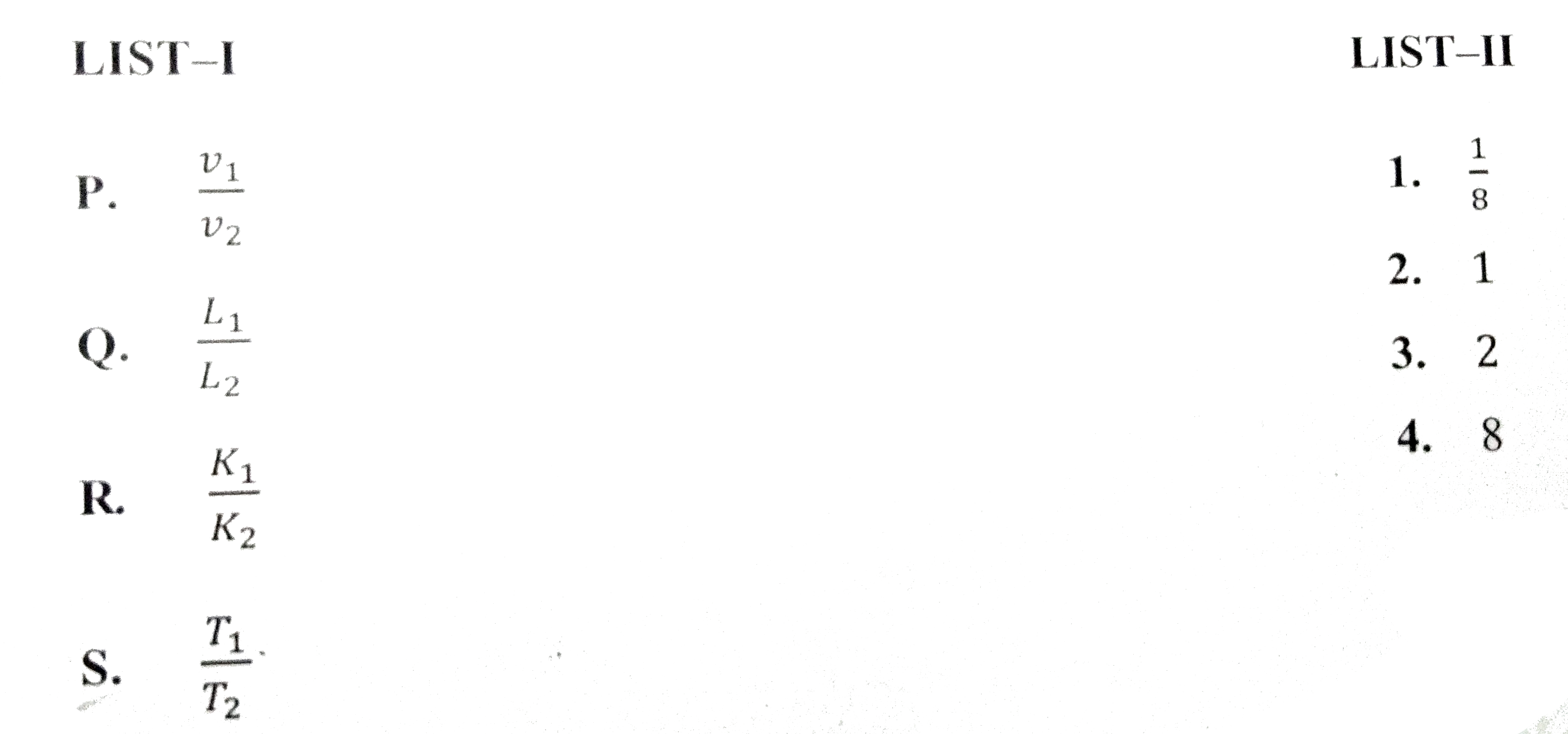
View SolutionTwo stars of masses m1 and m2 form a binary system,revolving around each other in circular orbits of radii r1 and r2 respectively.Time period of revolution for this system is

View Solution
Knowledge Check
Two satellite fo masses m and 4m orbit the earth in circular orbits of radii 4r and r respectively. The ratio of their orbital speed is
A1B12C1√2D1√5Two satellites of masses 3 m and m orbit the earth in circular orbits of radii r and 3 r respectively. The ratio of the their speeds is
A1:1B√3:1C3:1D9:1A binary star system consists of two stars of masses M1 and M2 revolving in circular orbits of radii R1 and R2 respectively. If their respective time periods are T1 and T2, then
AT1>T2 if R1>R2BT1>T2 if M1>M2CT1=T2DT1T2=(R1R2)3/2
Two satellites of same mass are launched in circular orbits at height of 2R and 3R respectively. The ration of kinetic energies is
View SolutionTwo satellites P and Q go round a planet in circular orbits of radii 9R and R respectively. If the speed of the satellite P is 4V, then speed of satellite Q will be
View SolutionTwo satellite A and B go round a planet P in circular orbits having radii 4R and R respectively. If the speed of the satellite A is 3v, the speed of the satellite B will be
View SolutionTwo satellites A and B go around a planet in circular orbits of radii 4 R and R respectively. If the speed of the satellite A is 3 V, then the speed of the satellite B will be
View SolutionTwo planets move around the sun. The periodic times and the mean radii of the orbits are T1,T2 and r1r2 respectively. The ratio T1/T2 is equal to
View Solution
