A straight of length L extends from x=a to x=L+a. the gravitational force it exerts on a point mass 'm' at x=0, if the mass per unit length of the rod is A+Bx2, is given by :
Gm[A(1a+L−1a)−BL]
Gm[A(1a−1a+L)−BL]
Gm[A(1a+L−1a)+BL]
Gm[A(1a−1a+L)−BL]
The correct Answer is:B
dm=rdx=(A+Bx2)dx
F=∫a+LaGmDMx2=GM∫a+La(A+Bx2)dxx2
=GM[∫a+LaAx2dx+a∫a+LaBdx]
F=4m[A(1a−1a+L)]+BL =GM[A(La(a+l))+Bl]

Similar Questions
A straight rod of length L has one of its end at the origin and the other at X=L. If the mass per unit length of the rod is given by Ax where A is constant, where is its centre of mass?
View SolutionFind the gravitatinal force of between a point mass m placed at a disance x on the prolongation of a thin rod of mass M andlength l from near end .
View Solution
Knowledge Check
A straight rod of length L extends from x=a to x=L+a. Find the gravitational force exerts on a point mass m at x=0 is (if the linear density of rodμ=A+Bx2)
AGm[Aa+BL]BGm[A(1a−1a+L)+BL]CGm[BL+Aa+L]DGm[BL−Aa]A straight rod of length 'l' extends from x=l to x=2l. If linear mass density of rod is μ=(μ0l3X3), then the gravitational force exerted by rod on a particle of mass m at x=0 , is
A12Gμ0mlBGμ0mlC32Gμ0mlD2Gμ0mlFind the potential energy of the gravitational interaction of a point mass m and a rod of mass m and length l, if they are along a straight line. Point mass is at a distance of a from the end of the rod.

Find the potential energy of the gravitationalAU=−Gm2lln(2a+l2a−l)BU=−Gm2l2ln(2a+l2a−l)CU=−Gm2l2ln(2a−l2a+l)DU=−Gm2l2ln(2a−l2a+l)2
Find the gravitational force between a point like mass M and an infinitely long, thin rod, of mass density ρ, which is at a distance L from the mass M.
View SolutionFind the potential energy of the gravitational interation of a point mass of mass m and a thin uniform rod of mass M and length l, if they are located along a straight line such that the point mass is at a distance 'a' from one end. Also find the force of their interaction.
View SolutionCalculate the force exerted by point mass m on rod of uniformly distributed mass M and length l (Placed as shown in figure)
 .
.
View SolutionThe gravitational force of attraction between a uniform sphere of mass M and a uniform rod of length l and mass in as shown in figure is
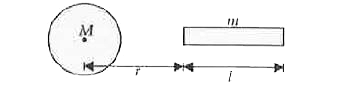
View SolutionChoose the most appropriate option.
The potential energy of gravitational interaction of a point mass m and a thin uniform rod of mass M and length L, if they are located along a straight line at a distance a from each other, is
View Solution