Satellites A and B are revolving around the earth. The mass of A is 10 times to mass of B. The ratio of time period (TATB) is x. Find x.
To solve the problem, we need to find the ratio of the time periods of two satellites A and B revolving around the Earth, given that the mass of satellite A is 10 times the mass of satellite B.
1. Understanding the Time Period of a Satellite:
The time period T of a satellite revolving around a planet can be derived from the gravitational force acting on it and the centripetal force required for circular motion. The formula for the time period is given by:
T=2π√R3GM
where R is the distance from the center of the Earth to the satellite, G is the gravitational constant, and M is the mass of the Earth.
2. Identifying the Variables:
- Let TA be the time period of satellite A.
- Let TB be the time period of satellite B.
- The mass of satellite A is mA=10mB, but the mass of the satellites does not affect the time period formula.
3. Applying the Time Period Formula:
Since both satellites are orbiting the Earth at the same distance R (assuming they are at the same orbital radius), we can write:
TA=2π√R3GMandTB=2π√R3GM
4. Finding the Ratio of Time Periods:
The ratio of the time periods TATB can be calculated as follows:
TATB=2π√R3GM2π√R3GM=1
5. Conclusion:
Therefore, the ratio x of the time periods TATB is:
x=1
Final Answer:
The value of x is 1.
The time period T of a satellite revolving around a planet can be derived from the gravitational force acting on it and the centripetal force required for circular motion. The formula for the time period is given by:
T=2π√R3GM
where R is the distance from the center of the Earth to the satellite, G is the gravitational constant, and M is the mass of the Earth.
- Let TA be the time period of satellite A.
- Let TB be the time period of satellite B.
- The mass of satellite A is mA=10mB, but the mass of the satellites does not affect the time period formula.
Since both satellites are orbiting the Earth at the same distance R (assuming they are at the same orbital radius), we can write:
TA=2π√R3GMandTB=2π√R3GM
The ratio of the time periods TATB can be calculated as follows:
TATB=2π√R3GM2π√R3GM=1
Therefore, the ratio x of the time periods TATB is:
x=1
The value of x is 1.
Similar Questions
Two satellites A and B are orbiting around the earth in ciruclar orbits of the same radius. The mass of A is 16 times that of B. Then the raito of the period of revolution of B to that of A is
View SolutionTwo satellites A and B are orbiting around the earth in ciruclar orbits of the same radius. The mass of A is 16 times that of B. Then the raito of the period of revolution of B to that of A is
View Solution
Knowledge Check
Two satellites are in the parking orbits around the earth. Mass of one is 5 times that of the other. The ratio of their periods of revolution is
A25B√5C1D3√5Two satellites A and B are orbiting around the earth in ciruclar orbits of the same radius. The mass of A is 16 times that of B. Then the raito of the period of revolution of B to that of A is
A1:16B1:4C1:2D1:1Satellite revolving around the earth at a height of 400 Km above the earth's surface has a time period of about
A24 hoursB90 minutesC2 hoursD>24 hours
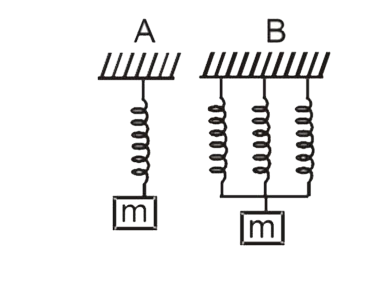
The springs in fig. A and B are identical but length in A is three times each of that in B. The ratio of period TA/TB is
View SolutionShow that period of a satellite revolving around the Earth depends upon mass of the Earth.
View SolutionShow that period of a satellite revolving around the Earth depends upon mass of the Earth.
View SolutionA satellite is revolving around the earth. Ratio of its orbital speed and escape speed will be.
View SolutionTwo satellites are revolving around the earth in circular orbits of same radii. Mass of one satellite is 100 times that of the other. Then their periods of revolutions are in the ratio
View Solution

